Question

A string in a musical instrument is $50cm$ long and its fundamental frequency is $800Hz$. If a frequency of $1000Hz$ is to be produced, then the required length of string is.
A. $37.5cm$
B. $40cm$
C. $50cm$
D. $62.5cm$

Answer 1

Hint:We know the frequency produced by a vibrating string is inversely proportional to the length of the string. $f \propto \dfrac{1}{L}$
By using this relation we can find the length of the string for any frequency.

Complete step-by-step answer:
First we find the relation between length of the string and wavelength of the wave produced.
Let us assume the length of the string is $L$ which tight between two point ${S_1}$, ${S_2}$ as shown in figure then the fundamental tone produced by the string have wavelength $\lambda $ and frequency $f$ velocity of wave in string is $v$. Then

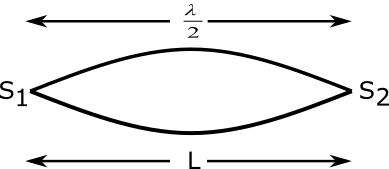
We can clearly see from figure the length of the string equal to the $\dfrac{\lambda }{2}$
$ \Rightarrow L = \dfrac{\lambda }{2}$
Wavelength of fundamental wave produced
$ \Rightarrow \lambda = 2L$ ........... (1)
We know the relation between velocity, wavelength and frequency of wave is
$ \Rightarrow v = f \times \lambda $
So the frequency of wave
$ \Rightarrow f = \dfrac{v}{\lambda }$
Put value of $\lambda $ from eq (1)
$ \Rightarrow f = \dfrac{v}{{2L}}$
So in his step we get the relation between frequency and length of the string. Velocity of the wave is constant for a string. So we can write.
$\therefore f\propto \dfrac{1}{L}$ ................ (2)
Step 2
From equation (2) we can write.
${f_1}\propto \dfrac{1}{{{L_1}}}$ ....... (3)
${f_2}\propto \dfrac{1}{{{L_2}}}$ ...... (4)
Divide (3) by (4)
$ \Rightarrow \dfrac{{{f_1}}}{{{f_2}}} = \dfrac{{{L_2}}}{{{L_1}}}$
$ \Rightarrow {L_2} = \dfrac{{{f_1}}}{{{f_2}}}\left( {{L_1}} \right)$
Now we take value which given in question
${f_1} = 800Hz$ ${L_1} = 50cm$
${f_2} = 1000Hz$
From these values we can calculate the length of string $\left( {{L_2}} \right)$for 1000Hz.
$ \Rightarrow {L_2} = \dfrac{{{f_1}}}{{{f_2}}}\left( {{L_1}} \right)$
$ \Rightarrow {L_2} = \dfrac{{800}}{{1000}}\left( {50cm} \right)$
Further solving it.
$ \Rightarrow {L_2} = 40cm$
So now we get the length of the string which can produce $1000Hz$ frequency.
$\therefore {L_2} = 40cm$

Hence in this question option B is correct.

Note:
We use in above question the velocity of wave in string is constant how it is constant the velocity wave in string is given by $v = \sqrt {\dfrac{T}{m}} $
Where $T \Rightarrow $ tension in the string
$m \Rightarrow $ Mass per unit length of string.
We did not change the string in the above question so we take the velocity of the wave as constant.