Question

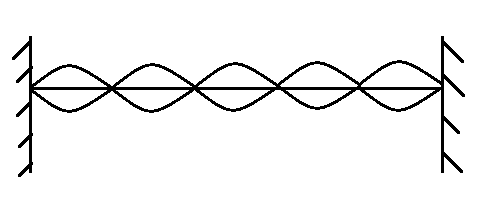
A string fixed at its both ends vibrates in 5 loops as shown in the figure. The total number of nodes and antinodes are respectively:

$A)\text{ }5,6$
$B)\text{ 6,5}$
$C)\text{ 7},4$
$D)\text{ 4},7$

Answer 1

Hint: A string fixed at its both ends when vibrates can produce standing waves which have alternate points of nodes and antinodes. Nodes are the points on the string where the displacement perpendicular to the length of the string is zero, that is, the point remains stationary whereas at the antinodes, the displacement is maximum.

Complete answer:
The string fixed at its both ends, when vibrating, is producing standing waves. Standing waves have alternate points of nodes and antinodes. At nodes, the displacement of the point transverse to the string is zero whereas at the antinodes, it is maximum. Therefore, the nodes do not show any movement throughout the wave motion.

In the figure, it can be clearly seen that there are points in the loops which are at the top (maximum displacement from the baseline). These are the mid points of the loops and also there are points which do not get displaced at all (the nodes between two loops).

By counting the number of points we can see that the number of antinodes is five while the number of nodes is six.
A figure is shown below marking one of the nodes and one of the antinodes for easy reference.

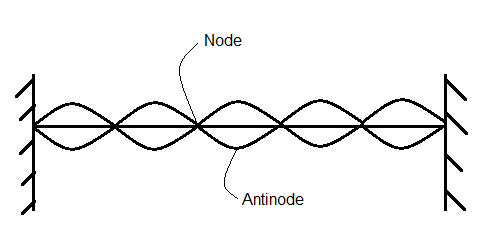
Therefore, the correct option is $\text{ 6,5}$.

So, the correct answer is “Option B”.

Note:
Students can also keep in mind that it is a general rule of thumb that for a standing wave, the number of antinodes is equal to the number of loops that are formed while the number of nodes is equal to one greater than the number of loops (that is, one greater than the number of antinodes). Antinodes are the points on the wave where there is constructive interference while the nodes are the points where there is destructive interference.