Question

A straight rod of length \[L\] extends from \[x=0\] to \[x=L\]. The variation of linear mass density of the rod with \[x\] co-ordinate is \[\lambda ={{a}_{0}}+{{b}_{0}}{{x}^{2}}\]. What is the gravitational force experienced by a point mass \[m\] at \[x=-a\]?
A. \[Gm\left( \dfrac{{{a}_{0}}}{a}+{{b}_{0}}L \right)\]
B. \[Gm\left[ {{a}_{0}}\left( \dfrac{1}{a}-\dfrac{1}{a+L} \right)+{{b}_{0}}L+{{b}_{0}}{{a}^{2}}\left( \dfrac{1}{a}-\dfrac{1}{a+L} \right)+2a{{b}_{0}}\ln \left( \dfrac{a+L}{a} \right) \right]\]
C. \[Gm\left( {{b}_{0}}L+\dfrac{{{a}_{0}}}{a+L} \right)\]
D. None of these

Answer 1

Hint: Use gravitation law to find the answer. It is better to consider a small region on the road. Since the mass density is varying along the x-coordinate, the variation of mass can find out from the linear density and distance between the point mass and the region. So, we can split the rod as infinite small regions. At last, we have to integrate these small regions to find the net force acting on the point mass.
Formula used:
\[F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\], where \[G\] is the gravitational constant, \[{{m}_{1}}\] and \[{{m}_{2}}\] are the masses of the objects and \[r\] is the distance between the objects.

Complete step-by-step answer:
 According to Newton’s law of gravitation, gravitational force can be written as,
\[F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\], where \[G\] is the gravitational constant, \[{{m}_{1}}\] and \[{{m}_{2}}\] are the masses of the objects and \[r\] is the distance between the objects.

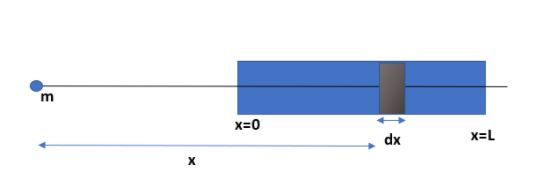
Here we are considering a straight rod of length \[L\]. The mass density of the rod is given.
\[\lambda ={{a}_{0}}+{{b}_{0}}{{x}^{2}}\]
Consider a small element \[dx\] at a distance \[x\]from \[x=0\]
Here the change in mass is directly proportional to the change in distance between the point and the considered small region in the rod.
\[dm=\lambda dx\]
We can assign the linear density that is already given in the question.
\[\lambda ={{a}_{0}}+{{b}_{0}}{{x}^{2}}\]
So, the change in mass will be,
\[dm=({{a}_{0}}+{{b}_{0}}{{x}^{2}})dx\]
We can assign this changing mass into the force equation.
\[dF=\dfrac{Gmdm}{{{x}^{2}}}\]
We can integrate this to find the force on the point due to the entire rod.
\[F=\int\limits_{a}^{a+L}{\dfrac{Gm}{{{x}^{2}}}({{a}_{0}}+{{b}_{0}}{{x}^{2}})dx}\]
\[F={{a}_{0}}Gm\int\limits_{a}^{a+L}{\dfrac{1}{{{x}^{2}}}dx+{{b}_{0}}Gm\int\limits_{a}^{a+L}{\dfrac{{{x}^{2}}dx}{x}}}\]
Hence the force will be,
\[F={{a}_{0}}Gm\left[ \dfrac{-1}{x} \right]_{a}^{a+L}+{{b}_{0}}Gm\left[ x \right]_{a}^{a+L}\]
Put the limits to the function.
\[F=Gm\left[ {{a}_{0}}\left[ \dfrac{1}{a}-\dfrac{1}{(a+L)} \right]+{{b}_{0}}(a+L-a) \right]\]
\[F=Gm\left[ \left[ \dfrac{{{a}_{0}}L}{a(a+L)} \right]+{{b}_{0}}L \right]\]

So, the correct option is D.

Note: Here we are taking the limit as \[a\] to \[a+L\]. The point is situated at a distance \[a\] from the rod. So, we have to add this distance in the limit if we are considering \[x\] as the distance between the considering region and the point. If we are taking the limit from 0 to \[L\], then we have to take \[x=a+L\].