Question

A straight line through the point \[\left( {h,k} \right)\] where \[h > 0\] and\[k > 0\], makes positive intercepts on the coordinate axes. Then the minimum length of the line intercepted between the coordinate axes is
A.\[{\left( {{h^{\dfrac{2}{3}}} + {k^{\dfrac{2}{3}}}} \right)^{\dfrac{3}{2}}}\]
B.\[{\left( {{h^{\dfrac{3}{2}}} + {k^{\dfrac{3}{2}}}} \right)^{\dfrac{2}{3}}}\]
C.\[{\left( {{h^{\dfrac{2}{3}}} - {k^{\dfrac{2}{3}}}} \right)^{\dfrac{3}{2}}}\]
D.\[{\left( {{h^{\dfrac{3}{2}}} - {k^{\dfrac{3}{2}}}} \right)^{\dfrac{2}{3}}}\]

Answer 1

Hint: Here in this given equation, we have to find the minimum length of the line intercept between the coordinate axes. To find this first, we have to find the coordinates of intercept line using a equation of line having slope m i.e., \[y - {y_1} = m\left( {x - {x_1}} \right)\] at the point \[\left( {h,k} \right)\]. Next by using a distance formula we get the equation of length of the intercept line and further differentiating the equation of length we get the required solution.

Complete step by step solution:
Now consider equation of line having slope m i.e., \[y - {y_1} = m\left( {x - {x_1}} \right)\]
The equation of line and passing through point \[\left( {h,k} \right)\] is given by:
\[ \Rightarrow y - k = m\left( {x - h} \right)\] -----(1)
Let the line intersects x-axis at A i.e., \[y = 0\], then equation (1) becomes
\[ \Rightarrow 0 - k = m\left( {x - h} \right)\]
\[ \Rightarrow - \dfrac{k}{m} = x - h\]
\[ \Rightarrow x = h - \dfrac{k}{m}\]
Co-ordinates of A are \[\left( {h - \dfrac{k}{m},0} \right)\]
Let the line intersects y-axis at B i.e., \[x = 0\], then equation (1) becomes
\[ \Rightarrow y - k = m\left( {0 - h} \right)\]
\[ \Rightarrow y - k = - mh\]
\[ \Rightarrow y = k - mh\]
Coordinates of B are \[\left( {0,k - mh} \right)\]

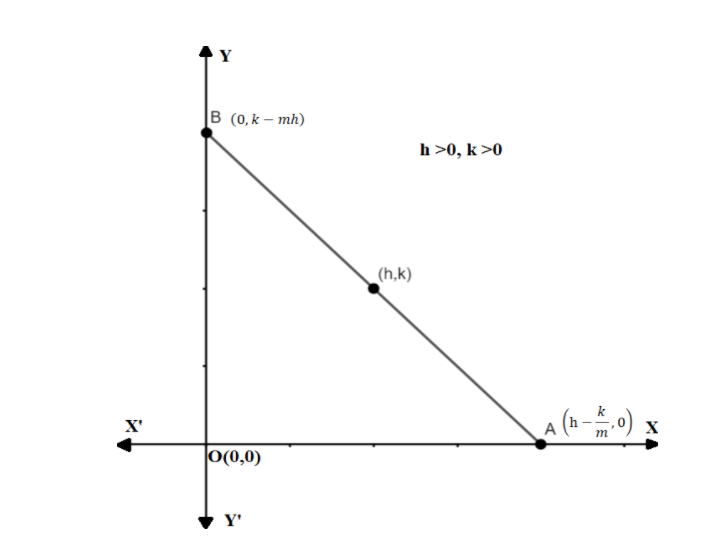
Now, find the Length of line intercepted between coordinate AB by using a distance formula i.e., \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \], then
\[ \Rightarrow AB = \sqrt {{{\left( {0 - \left( {h - \dfrac{k}{m}} \right)} \right)}^2} + {{\left( {k - mh - 0} \right)}^2}} \]
\[ \Rightarrow AB = \sqrt {{{\left( {h - \dfrac{k}{m}} \right)}^2} + {{\left( {k - mh} \right)}^2}} \]
Taking square on both sides, we have
\[ \Rightarrow A{B^2} = {\left( {h - \dfrac{k}{m}} \right)^2} + {\left( {k - mh} \right)^2}\]
The above equation is the function of m then it can be written as
\[ \Rightarrow f\left( m \right) = {\left( {h - \dfrac{k}{m}} \right)^2} + {\left( {k - mh} \right)^2}\]------(2)
Now, to find the maximum of minimum, we have to find the \[f'\left( m \right)\] it should be 0 at maxima or minima i.e.,
\[ \Rightarrow f'\left( m \right) = 0\]
Now, differentiate the equation (2), with respect to m, using a standard differentiation formula \[\dfrac{d}{{dx}}\left( {{x^2}} \right) = 2x\]
 \[ \Rightarrow f'\left( m \right) = 2\left( {\dfrac{k}{{{m^2}}}} \right)\left( {h - \dfrac{k}{m}} \right) + 2\left( { - h} \right)\left( {k - mh} \right) = 0\]
\[ \Rightarrow \dfrac{{2k}}{{{m^2}}}\left( {h - \dfrac{k}{m}} \right) + 2h\left( {mh - k} \right) = 0\]
\[ \Rightarrow \dfrac{{2k}}{{{m^2}}}\left( {\dfrac{{mh - k}}{m}} \right) + 2h\left( {mh - k} \right) = 0\]
\[ \Rightarrow \dfrac{{2k}}{{{m^3}}}\left( {mh - k} \right) + 2h\left( {mh - k} \right) = 0\]
Take out \[\left( {mh - k} \right)\] as common, then we get
\[ \Rightarrow \left( {mh - k} \right)\left( {\dfrac{{2k}}{{{m^3}}} + 2h} \right) = 0\]
Equate each term with zero
\[ \Rightarrow \left( {mh - k} \right) = 0\] and \[\left( {\dfrac{{2k}}{{{m^3}}} + 2h} \right) = 0\]
\[ \Rightarrow mh - k = 0\] \[\dfrac{{2k}}{{{m^3}}} = - 2h\]
\[ \Rightarrow mh = k\] \[\dfrac{{2k}}{{ - 2h}} = {m^3}\]
\[ \Rightarrow m = \dfrac{k}{h}\] \[m = {\left( { - \dfrac{k}{h}} \right)^{\dfrac{1}{3}}}\]
As we know, for maxima \[f'\left( m \right) > 0\] and for minima \[f'\left( m \right) \leqslant 0\]
Hence, \[f\left( m \right)\] has a minimum at \[m = {\left( { - \dfrac{k}{h}} \right)^{\dfrac{1}{3}}}\]
Now, find the minimum length by substituting m in equation (2)
\[m = - \dfrac{{{k^{\dfrac{1}{3}}}}}{{{h^{\dfrac{1}{3}}}}}\]
Divide both numerator and denominator by k then
\[m = - \dfrac{{k \cdot {k^{\dfrac{1}{3}}}}}{{k \cdot {h^{\dfrac{1}{3}}}}} = \dfrac{{k \cdot {k^{\dfrac{1}{3} - 1}}}}{{{h^{\dfrac{1}{3}}}}} = - \dfrac{{k \cdot {k^{ - \dfrac{2}{3}}}}}{{{h^{\dfrac{1}{3}}}}}\]
On cross multiplying, we have
\[\dfrac{k}{m} = - \dfrac{{{h^{\dfrac{1}{3}}}}}{{{k^{ - \dfrac{2}{3}}}}} = - {h^{\dfrac{1}{3}}} \cdot {k^{\dfrac{2}{3}}}\]-----(a)

Again take \[m = - \dfrac{{{k^{\dfrac{1}{3}}}}}{{{h^{\dfrac{1}{3}}}}}\]
Divide both numerator and denominator by h then
\[m = - \dfrac{{h \cdot {k^{\dfrac{1}{3}}}}}{{h \cdot {h^{\dfrac{1}{3}}}}} = \dfrac{{{k^{\dfrac{1}{3}}}}}{{h \cdot {h^{\dfrac{1}{3} - 1}}}} = - \dfrac{{{k^{\dfrac{1}{3}}}}}{{h \cdot {h^{ - \dfrac{2}{3}}}}}\]
On cross multiplying, we have
\[mh = - \dfrac{{{k^{\dfrac{1}{3}}}}}{{{h^{ - \dfrac{2}{3}}}}} = {k^{\dfrac{1}{3}}} \cdot {h^{\dfrac{2}{3}}}\]-------(b)
Now consider equation (2)
\[ \Rightarrow f\left( m \right) = {\left( {h - \dfrac{k}{m}} \right)^2} + {\left( {k - mh} \right)^2}\]
Substitute equation (a) and (b), then
\[ \Rightarrow f\left( m \right) = {\left( {h - \left( { - {h^{\dfrac{1}{3}}} \cdot {k^{\dfrac{2}{3}}}} \right)} \right)^2} + {\left( {k - \left( { - {k^{\dfrac{1}{3}}} \cdot {h^{\dfrac{2}{3}}}} \right)} \right)^2}\]
\[ \Rightarrow f\left( m \right) = {\left( {h + {h^{\dfrac{1}{3}}} \cdot {k^{\dfrac{2}{3}}}} \right)^2} + {\left( {k + {k^{\dfrac{1}{3}}} \cdot {h^{\dfrac{2}{3}}}} \right)^2}\]
Expand each term by using a algebraic identity \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\], then we have
\[ \Rightarrow f\left( m \right) = {h^2} + {\left( {{h^{\dfrac{1}{3}}} \cdot {k^{\dfrac{2}{3}}}} \right)^2} + 2 \cdot h \cdot {h^{\dfrac{1}{3}}} \cdot {k^{\dfrac{2}{3}}} + {k^2} + {\left( {{k^{\dfrac{1}{3}}} \cdot {h^{\dfrac{2}{3}}}} \right)^2} + 2 \cdot k \cdot {k^{\dfrac{1}{3}}} \cdot {h^{\dfrac{2}{3}}}\]
\[ \Rightarrow f\left( m \right) = {h^2} + {h^{\dfrac{2}{3}}} \cdot {k^{\dfrac{4}{3}}} + 2 \cdot {h^{1 + \dfrac{1}{3}}} \cdot {k^{\dfrac{2}{3}}} + {k^2} + {k^{\dfrac{2}{3}}} \cdot {h^{\dfrac{4}{3}}} + 2 \cdot {k^{1 + \dfrac{1}{3}}} \cdot {h^{\dfrac{2}{3}}}\]
\[ \Rightarrow f\left( m \right) = {h^2} + {h^{\dfrac{2}{3}}} \cdot {k^{\dfrac{4}{3}}} + 2 \cdot {h^{\dfrac{4}{3}}} \cdot {k^{\dfrac{2}{3}}} + {k^2} + {k^{\dfrac{2}{3}}} \cdot {h^{\dfrac{4}{3}}} + 2 \cdot {k^{\dfrac{4}{3}}} \cdot {h^{\dfrac{2}{3}}}\]
 \[ \Rightarrow f\left( m \right) = {h^2} + 3 \cdot {h^{\dfrac{4}{3}}} \cdot {k^{\dfrac{2}{3}}} + {k^2} + 3 \cdot {k^{\dfrac{4}{3}}} \cdot {h^{\dfrac{2}{3}}}\]
It can be written as
\[ \Rightarrow f\left( m \right) = {\left( {{h^{\dfrac{2}{3}}}} \right)^3} + {\left( {{k^{\dfrac{2}{3}}}} \right)^3} + 3 \cdot {h^{\dfrac{2}{3}}} \cdot {k^{\dfrac{2}{3}}}\left( {{h^{\dfrac{2}{3}}} + {k^{\dfrac{2}{3}}}} \right)\]
The above equation similar as a algebraic identity \[{\left( {a + b} \right)^3} = {a^3} + {b^3} + 3ab\left( {a + b} \right)\]
Here, \[a = {h^{\dfrac{2}{3}}}\] , \[b = {k^{\dfrac{2}{3}}}\], and \[f\left( m \right) = A{B^2}\]
\[ \Rightarrow A{B^2} = {\left( {{h^{\dfrac{2}{3}}} + {k^{\dfrac{2}{3}}}} \right)^3}\]
Taking square root on both side, we get
\[ \Rightarrow A{B^2} = {\left( {{h^{\dfrac{2}{3}}} + {k^{\dfrac{2}{3}}}} \right)^{\dfrac{3}{2}}}\]
Hence, the minimum length of the line intercepted between the coordinate axes is \[A{B^2} = {\left( {{h^{\dfrac{2}{3}}} + {k^{\dfrac{2}{3}}}} \right)^{\dfrac{3}{2}}}\]
Therefore, option (A) is correct.
So, the correct answer is “Option A”.

Note: Remember, Let \[f\left( x \right)\] be any real valued function in an interval \[\left[ {a,b} \right]\] on which the function \[f\] is differentiable and considered \[c\] as critical point of function \[f\] in \[\left[ {a,b} \right]\]. If differentiable function \[f'\left( x \right) > 0\], then \[f'\left( c \right)\] will be considered as the maximum value of function \[f\] in the interval \[\left[ {a,b} \right]\] similarly if \[f'\left( x \right) \leqslant 0\], then \[f'\left( c \right)\] will be considered as the minimum value of function \[f\] in the interval \[\left[ {a,b} \right]\].