Question

A straight line through the point (2, 2) intersects the lines √3x + y = 0 and √3x – y = 0 at the point A and B. The equation to the line AB so that the triangle OAB is equilateral is:

Answer 1

Hint: Draw the given two lines then draw a line from the point (2, 2) such that it intersects at A & B. After drawing the lines, you will find one line is making 60° with the positive x axis and the other line is making 120° from the positive axis then see how the line through the point (2, 2) be adjusted so that OAB is equilateral.

Complete step-by-step answer:
In the below diagram, we have shown the straight lines √3x + y = 0 and √3x – y = 0 and a line passing through point (2, 2):

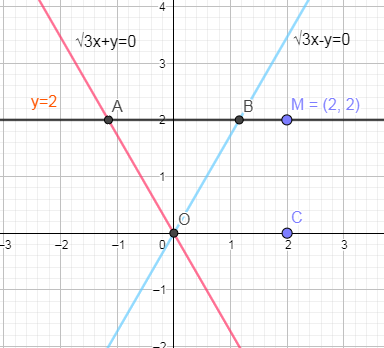
Now, from the above figure, we can see that angle made by the line √3x – y = 0 is 60° from the positive x axis because the slope of this line is √3 and tan θ = √3 so θ = 60°. Similarly we can find the angle made by the line √3x + y = 0 from the positive x axis and the angle is 120° so the angle made by the line √3x + y = 0 from negative x axis is 60° and so the$\angle AOB={{60}^{0}}$.
As, it is given that OAB is an equilateral triangle so all the angles must be 60°. So, for $\angle BAO\text{ and }\angle \text{ABO}$ to be 60° the equation of a line passing through (2, 2) should be parallel to the x axis.
When the line passing through (2, 2) is parallel to x axis then $\angle ABO=\angle BOC={{60}^{0}}$(alternate interior angles) and we know that sum of all the angles of a triangle is 60° so as we have shown above that sum of $\angle AOB\text{ and }\angle \text{ABO}$ is equal to 120° then the $\angle BAO={{60}^{0}}$.
Hence, the equation of a line passing through (2, 2) is y = 2.

Note: The alternative of the above method is to first write the equation of a line passing through point (2, 2) and with a slope m.
$y-2=m\left( x-2 \right)$
And we have to find the slope m for writing the equation of a straight line. Then find the intersection of the line with the two lines. You will get the coordinates of A and B in m and as all the sides are equal so using the distance formula equate any two sides. From that, you will get the value of m and then put in the equation of a line.