Question

A straight line through \[P\left( 1,2 \right)\] is such that its intercept between the axes is bisected at P. Its equation is
(A) \[x+2y=5\]
(B) \[x-y+1=0\]
(C) \[x+y-3=0\]
(D) \[2x+y-4=0\]

Answer 1

Hint: We are given a line which passes through a point \[P\left( 1,2 \right)\] and that its intercept between the axes is bisected at P. We will first find the coordinates of the intercept of the given line. Then, we will find the value of the slope of the line using the formula, \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]. Using the straight line equation at point P, we will find the equation of the line.

Complete step by step solution:
According to the given question, we are given a line which passes through a point \[P\left( 1,2 \right)\] and that its intercept between the axes is bisected at P and we are asked to find the equation of the line.
The line passes through \[P\left( 1,2 \right)\] and so its intercepts bisect at P, that is,
\[\begin{align}
  & \dfrac{a+0}{2}=1 \\
 & \Rightarrow a=2 \\
\end{align}\]
\[\begin{align}
  & \dfrac{b+0}{2}=2 \\
 & \Rightarrow b=4 \\
\end{align}\]
So, we have the coordinates of the intercepts as,
\[\left( 0,4 \right)\] and \[\left( 2,0 \right)\]
We can name these coordinates as,
\[\left( 0,4 \right)\left( 2,0 \right)=\left( {{x}_{1}},{{y}_{1}} \right)\left( {{x}_{2}},{{y}_{2}} \right)\]
Now, we have to find the slope of the line using the formula, \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
\[\Rightarrow m=\dfrac{0-4}{2-0}\]
On solving, we will get the value of slope as,
\[\Rightarrow m=-2\]
We know that the general equation of a straight line is of the form, \[y=mx+c\].
So, the equation of the line at point \[P\left( 1,2 \right)\], will be,
\[y-2=\left( -2 \right)\left( x-1 \right)\]
\[\Rightarrow y-2=-2x+2\]
Rearranging the above expression, we have the expression as,
\[\Rightarrow 2x+y-4=0\]

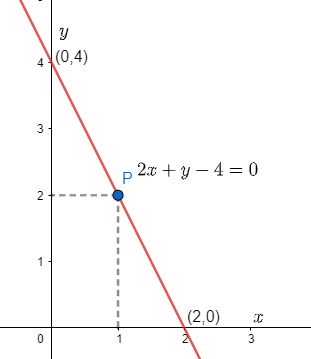
Therefore, the correct option is (D) \[2x+y-4=0\].

Note: The equation \[y=mx+c\] represents the linear equation where ‘m’ is the slope and ‘c’ is the y – intercept. Also, while carrying out the calculation, make sure that any terms are not missed out else the answer will come out wrong.