Question

A straight line L through the point $\left( 3,-2 \right)$ is inclined at an angle of ${{60}^{0}}$ to the line $\sqrt{3}x+y=1$. If L also intersects the $x-$ axis, then the equation of L is
(A). $y+\sqrt{3}x+2-3\sqrt{3}=0$
(B). $\sqrt{3}y-x+3+2\sqrt{3}=0$
(C). $\sqrt{3}y+x-3+2\sqrt{3}=0$
(D). $ y-\sqrt{3}x+2+3\sqrt{3}=0$

Answer 1

Hint: As the angle between line and one of slope of line is given so find the slope of another line can be found by using formula $\tan \theta =\left| \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right|$ as $\theta $ is the angle between them ${{m}_{1}}{{m}_{2}}$ are slopes. Then use the formula $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the point m is slope to find another line.

Complete step-by-step solution -
We are given a straight line L which passes through the point $\left( 3,-2 \right)$ is inclined at an angle ${{60}^{0}}$ to the line $\sqrt{3}x+y=1$. It is also said that line L passes through the $x-$ axis.
If the two straight lines are given in form of $y={{m}_{1}}x+{{c}_{1}}$ $y={{m}_{2}}x+{{c}_{2}}$ then the angle between them be $\theta $, then we can say that
$\tan \theta =\pm \dfrac{\left( {{m}_{2}}-{{m}_{1}} \right)}{\left( 1+{{m}_{1}}{{m}_{2}} \right)}$
Let us draw the figure,

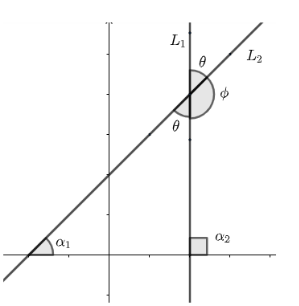
Let the measurement of $\tan {{\alpha }_{1}}$ be ${{m}_{1}}$ and $\tan {{\alpha }_{2}}$ be ${{m}_{2}}$, so $\theta $ can be represented as ${{\alpha }_{2}}-{{\alpha }_{1}}$.
So, $\tan \theta =\tan \left( {{\alpha }_{2}}-{{\alpha }_{1}} \right)$
Now using formula $\tan \left( {{\alpha }_{2}}-{{\alpha }_{1}} \right)=\dfrac{\tan {{\alpha }_{2}}-\tan {{\alpha }_{1}}}{1+\tan {{\alpha }_{1}}\tan {{\alpha }_{2}}}$ to expand we get,
$\tan \theta =\dfrac{\tan \left( {{\alpha }_{2}} \right)-\tan \left( {{\alpha }_{1}} \right)}{1+\tan {{\alpha }_{1}}\tan {{\alpha }_{2}}}$
Now substituting $\tan {{\alpha }_{1}}$ as ${{m}_{1}}$ and $\tan {{\alpha }_{2}}$ as ${{m}_{2}}$, we get,
$\tan \theta =\dfrac{\left( {{m}_{2}}-{{m}_{1}} \right)}{\left( 1+{{m}_{1}}{{m}_{2}} \right)}$
As $\theta $ should be acute so $\tan \theta $ becomes,
$\theta ={{\tan }^{-1}}\left( \left| \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right| \right)$
In the question it was given that the angle between lines is ${{60}^{0}}$, so here $\theta $ is ${{60}^{0}}$. And we know one of the line which is $\sqrt{3}x+y=1$ which can be represented as $y=-\sqrt{3}x+1$
So, the slope of the line is $-\sqrt{3}$ because if a line is given in the form of $y=mx+c$ then its slope will be “$m$”.
Now let ${{m}_{1}}=-\sqrt{3}$ so by using the formula, we get
$\tan \theta =\left( \left| \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right| \right)$
We will be substitute ${{m}_{1}}=-\sqrt{3}$ and $\theta ={{60}^{0}}$ we get,
$\tan {{60}^{0}}=\left( \left| \dfrac{{{m}_{2}}+\sqrt{3}}{1-\sqrt{3}{{m}_{2}}} \right| \right)$
So, we can write the above expression as,
 $\pm \sqrt{3}=\dfrac{{{m}_{2}}+\sqrt{3}}{1-\sqrt{3}{{m}_{2}}}$
There are two cases in the above expression, one the value of $\dfrac{\left( {{m}_{2}}+\sqrt{3} \right)}{\left( 1-\sqrt{3}{{m}_{2}} \right)}$ is $\sqrt{3}$ and in other the value is $-\sqrt{3}$.
Let’s take 1st case which is,
$\sqrt{3}=\dfrac{{{m}_{2}}+\sqrt{3}}{1-\sqrt{3}{{m}_{2}}}$
On cross multiplication we get
$\sqrt{3}-3{{m}_{2}}={{m}_{2}}+\sqrt{3}$
$\Rightarrow 4{{m}_{2}}=0$
Hence ${{m}_{2}}=0$
Let’s take 2nd case which is,
$-\sqrt{3}=\dfrac{{{m}_{2}}+\sqrt{3}}{1-\sqrt{3}{{m}_{2}}}$
On cross multiplication we get,
$-\sqrt{3}+3{{m}_{2}}={{m}_{2}}+\sqrt{3}$
$\Rightarrow 2{{m}_{2}}=2\sqrt{3}$
Hence ${{m}_{2}}=\sqrt{3}$
The 1st case is not possible because the line also passes through $\left( 3,-2 \right)$
As the slope is $\sqrt{3}$ and point is $\left( 3,-2 \right)$ then we will find the line by using the formula,
$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ is point and $m$ is slope
$\Rightarrow y+2=\sqrt{3}\left( x-3 \right)$
On simplification we get,
$\begin{align}
  & y+2=\sqrt{3}x-3\sqrt{3} \\
 & \Rightarrow y-\sqrt{3}x+2+3\sqrt{3}=0 \\
\end{align}$
Hence the correct option is ”D”.

Note: The formula is only used for all the values except if the product of ${{m}_{1}}$ and ${{m}_{2}}$ is not equal to $-1$. Because then $1+{{m}_{1}}{{m}_{2}}$ will be equal to $''0''$ which makes the expression undefined. In that case $\theta $ is directly considered as ${{90}^{0}}$.