Question

A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of \[30^\circ \], which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be \[60^\circ \]. Find the time taken by the car to reach the foot of the tower from this point.

Answer 1

Hint: Here, we will first draw the triangle using the given conditions to simplify the calculation. Then use the tangential property, that is, \[\tan {\text{A}} = \dfrac{p}{b}\], where \[p\] is the perpendicular and \[b\] is the base. Apply this property, and then use the given conditions to find the required value.

Complete step by step answer:

Let us assume that the height of the tower is \[h\] and \[x\] and \[y\] are the distance of two points from the tower.

We are given that the time taken to cover the \[y\] distance is 6 seconds.

First, we will draw the triangle using the given conditions.

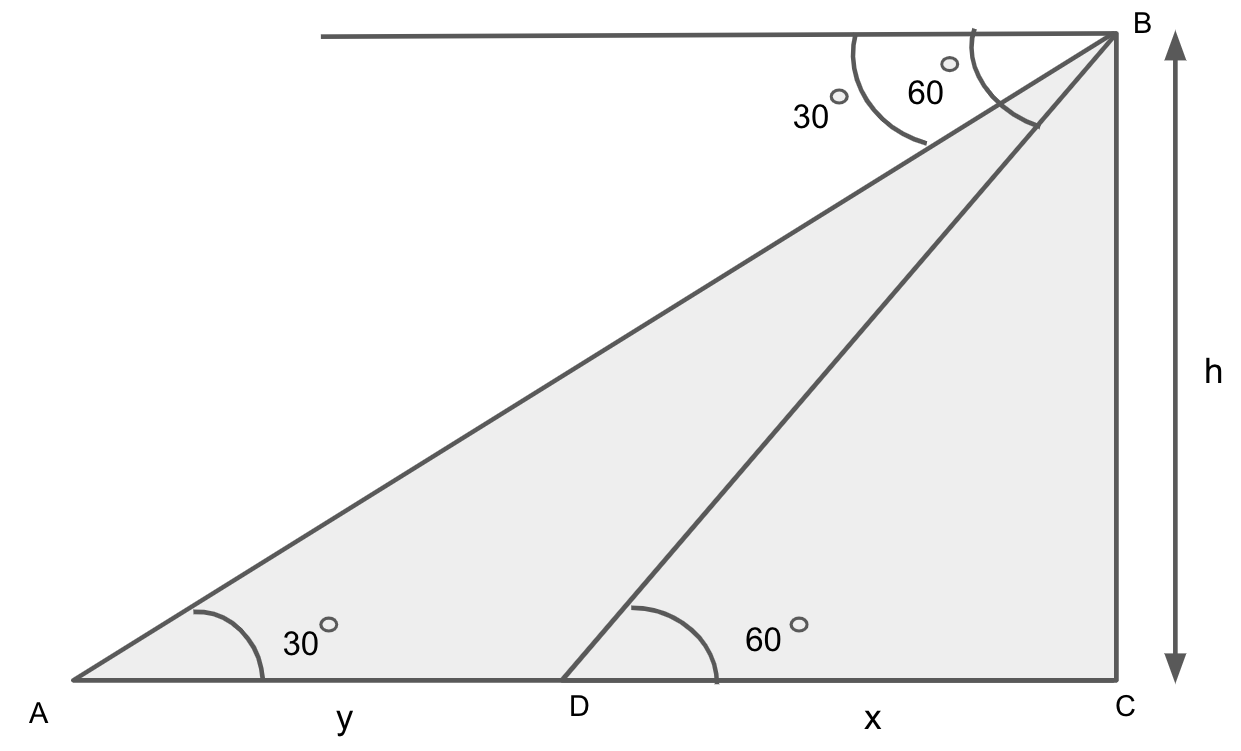
First, we will take the triangle \[\Delta {\text{ABC}}\].
We will use the tangential property, that is, \[\tan {\text{A}} = \dfrac{p}{b}\], where \[p\] is the perpendicular and \[b\] is the base.

Using the above tangential property, we get

\[\tan 30^\circ = \dfrac{{{\text{BC}}}}{{{\text{AC}}}}\]

Substituting the values of the length AC and BC in the above equation, we get

\[
   \Rightarrow \tan 30^\circ = \dfrac{h}{{x + y}} \\
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{x + y}} \\
 \]

Cross-multiplying the above equation, we get

\[ \Rightarrow x + y = \sqrt 3 h{\text{ ......eq.(1)}}\]

We will now take the triangle \[\Delta {\text{BCD}}\],

We will use the tangential property, that is, \[\tan {\text{A}} = \dfrac{p}{b}\], where \[p\] is the perpendicular and \[b\] is the base.

Using the above tangential property, we get

\[\tan 60^\circ = \dfrac{{{\text{BC}}}}{{{\text{CD}}}}\]

Substituting the values of the length BC and CD in the above equation, we get

\[
   \Rightarrow \tan 60^\circ = \dfrac{h}{x} \\
   \Rightarrow \sqrt 3 = \dfrac{h}{x} \\
 \]

Cross-multiplying the above equation, we get

\[\sqrt 3 x = h{\text{ ......eq.(2)}}\]

Using the equation \[\left( 2 \right)\] in the equation \[\left( 1 \right)\], we get
\[
   \Rightarrow x + y = \sqrt 3 \left( {\sqrt 3 x} \right) \\
   \Rightarrow x + y = 3x \\
 \]

Subtracting the above equation by \[x\] on both sides, we get

\[
   \Rightarrow x + y - x = 3x - x \\
   \Rightarrow y = 2x{\text{ .......eq.(3)}} \\
 \]

We know that the formula to find the speed is \[\dfrac{d}{t}\], where \[d\] is the distance and \[t\] is the time.

We also know that if speed is uniform than the speed to cover the distance \[x\] is equal to the speed to cover the distance \[x + y\] from the given diagram.

Then we have that the speed \[\dfrac{x}{t}\], where \[x\] is the distance and \[t\] is the time in the triangle BCD is equal to the speed \[\dfrac{{x + y}}{{6 + t}}\], where \[x + y\] is the distance and \[t + 6\] is the time in the triangle in the triangle ABC, we get

\[ \Rightarrow \dfrac{x}{t} = \dfrac{{x + y}}{{6 + t}}\]

Cross-multiplying the above equation, we get

\[
   \Rightarrow \left( {6 + t} \right)x = t\left( {x + y} \right) \\
   \Rightarrow 6x + tx = tx + ty \\
 \]

Using the equation \[(3)\] in the above equation, we get
\[
   \Rightarrow 6x + tx = tx + t\left( {2x} \right) \\
   \Rightarrow 6x + tx = tx + 2tx \\
   \Rightarrow 6x + tx = 3tx \\
 \]

Subtracting the above equation by \[tx\] on both sides, we get

\[
   \Rightarrow 6x + tx - tx = 3tx - tx \\
   \Rightarrow 6x = 2tx \\
 \]

Dividing the above equation by \[2x\] on each side, we get

\[
   \Rightarrow \dfrac{{6x}}{{2x}} = \dfrac{{3tx}}{{2x}} \\
   \Rightarrow 3 = t \\
   \Rightarrow t = 3 \\
 \]

Therefore, the time to cover \[x\] distance is 3 seconds.

Note: In solving these types of questions, you should be familiar with the concept of angle of depression and the tangential properties. Students should make the diagram for better understanding. Using the values of respective angles you can simply find any length present in the figure using the tangential value ‘\[\tan \]’, which makes our problem easy to solve.