Question

A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of \[{{30}^{\circ }}\] ,which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be \[{{60}^{\circ }}\] . Find the time taken by the car to reach the foot of the tower from this point.
\[(A)\text{ 3 sec}\]
\[(B)\text{ 4 sec}\]
\[(C)\text{ 2 sec}\]
\[(D)\text{ 6 sec}\]

Answer 1

Hint: In these types of questions, we will first draw diagrams to get clear understanding. As the tower is always perpendicular to the road, therefore the diagram will represent right angled triangles. WE will use the basic property of trigonometry in a right-angled triangle which is \[\text{tan}\theta =\dfrac{Perpendicular}{Base}\].

Complete step by step answer:
Let us first draw the diagram according to the question.
 

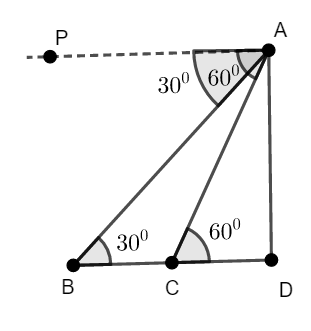
In the diagram, we have considered AD as the height of tower and man. B is the point where man saw the car first. C is the point where the man saw the car after 6 seconds. We have to find time taken by car to reach the foot of the tower, that is we have to calculate CD.
As we are given that man sees the car first at an angle of depression \[{{30}^{\circ }}\]. So \[\angle PAB={{30}^{\circ }}\].
After 6 seconds, the man sees the car at an angle of depression \[{{60}^{\circ }}\]. So, \[\angle PAC={{60}^{\circ }}\].
Since, we know the tower is perpendicular to the ground, therefore, \[\angle ADB={{90}^{\circ }}\].
Observing the diagram, we can see that PA is parallel to BD and AB and AC are transversal to them.
Taking AB as transversal, we can see that \[\angle ABD\]and \[\angle PAB\] are alternate interior angles and hence they are equal. Therefore,
\[\angle ABD=\angle PAB={{30}^{\circ }}\]
Taking AC as transversal, we can see that \[\angle ACD\] and \[\angle PAC\] are alternate interior angles and hence they are equal. Therefore,
\[\angle ACD=\angle PAC={{60}^{\circ }}\]
Hence, we got \[\angle ABD={{30}^{\circ }}\], \[\angle ACD={{60}^{\circ }}\].
In right triangle ACD, as we know
\[\text{tan}\theta =\dfrac{side\text{ }opposite\text{ }to\text{ }\theta }{side\text{ }adjacent\text{ }to\text{ }\theta }\]
\[\text{tan C}=\dfrac{AD}{CD}\]
\[\text{tan }{{60}^{\circ }}=\dfrac{AD}{CD}\]
We know that \[\text{tan }{{60}^{\circ }}=\sqrt{3}\]. Therefore,
\[\sqrt{3}=\dfrac{AD}{CD}\]
\[AD=\sqrt{3}CD\]……….. equation (1)
In right triangle ABD,
\[\text{tan B}=\dfrac{side\text{ }opposite\text{ }to\text{ }B}{side\text{ }adjacent\text{ }to\text{ }B}\]
\[\text{tan 3}{{0}^{\circ }}=\dfrac{AD}{BD}\]
We know that \[\text{tan 3}{{0}^{\circ }}=\dfrac{1}{\sqrt{3}}\] . therefore,
\[\dfrac{1}{\sqrt{3}}=\dfrac{AD}{BD}\]
\[AD=\dfrac{BD}{\sqrt{3}}\]……………. equation (2)
From equation (1) and equation (2), we can say that
\[\sqrt{3}CD=\dfrac{BD}{\sqrt{3}}\]
Cross multiplying,
\[\sqrt{3}(\sqrt{3}CD)=BD\]
\[3CD=BD\]
From diagram, we can see that
\[BC+CD=BD\]
\[3CD-CD=BC\]
\[2CD=BC\]
\[CD=\dfrac{BC}{2}\]
We are given that time taken to cover BC is 6 seconds and hence time taken to cover half of BC that is \[\dfrac{BC}{2}=\dfrac{6}{2}=3\sec \]. As we have calculated earlier, \[CD=\dfrac{BC}{2}\]. Therefore, time taken to cover \[CD=3\sec \].
Hence, it takes 3 seconds to reach the foot of the tower.

So, the correct answer is “Option A”.

Note: students should not get confused with angle of elevation and angle of depression. Also, they should take care while using the \[\text{tan }\theta \] formula. \[\text{tan }\theta \] is equal to perpendicularly divided by bases. Other formulas are\[\cos \theta =\dfrac{Base}{Hypotenuse}\] and \[sin\theta =\dfrac{Perpendicular}{Hypotenuse}\]. Students should learn Basic trigonometric values like \[\text{sin }{{0}^{\circ }}\],\[\text{sin 3}{{0}^{\circ }}\],\[\text{sin 4}{{\text{5}}^{\circ }}\],\[\text{sin 6}{{\text{0}}^{\circ }}\],\[\text{sin 9}{{\text{0}}^{\circ }}\], \[\text{cos }{{\text{0}}^{\circ }}\],\[\text{cos 3}{{\text{0}}^{\circ }}\],\[\text{cos 4}{{\text{5}}^{\circ }}\],\[\text{cos 6}{{\text{0}}^{\circ }}\],\[\text{cos 9}{{\text{0}}^{\circ }}\],\[\text{tan }{{\text{0}}^{\circ }}\],\[\text{tan 3}{{\text{0}}^{\circ }}\],\[\text{tan 4}{{\text{5}}^{\circ }}\],\[\text{tan 6}{{\text{0}}^{\circ }}\],\[\text{tan 9}{{\text{0}}^{\circ }}\].