Question

A straight conductor carries a current. Assume that all free electrons in the conductor move with the same drift velocity $ v $ . $ A $ and $ B $ are two observers on a straight line $ XY $ parallel to the conductor. $ A $ is stationary, $ B $ moves along $ XY $ with a velocity $ v $ in the direction of the free electrons.
(A) $ A $ and $ B $ observe the same magnetic field
(B) $ A $ observes a magnetic field, $ B $ does not
(C) $ A $ and $ B $ observe magnetic fields of the same magnitude but opposite directions
(D) $ A $ and $ B $ do not observe any electric field

Answer 1

Hint To solve this question, we need to use the concept of relative velocity for the charge carriers within the conductor. The charge carriers within any conductor are protons and electrons.

Complete step by step answer
Let the situation be as shown in the figure below. The black dots represent the electrons and the other species are the protons.

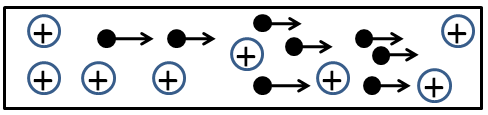
We know that an atom is electrically neutral. So, it has an equal number of electrons and protons. The current in a conductor is produced by the motion of the free electrons, while the protons remain at rest. So, for the observer $ B $ , who is at rest, the current will be in the opposite direction of $ v $ , that is, on the left. Let us say that this current is equal to $ I $ .
But for the observer $ A $ , who is moving with the same velocity $ v $ as that of the electron, the electrons will be at rest and the protons will move with a speed of $ v $ in the left direction. This is shown in the figure below.

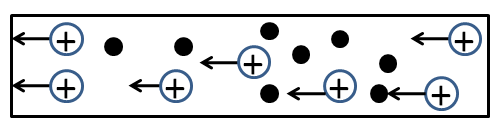
As the charge on a proton is the same as that on an electron, also the direction of the current is in the direction of motion of positive charges, so for the observer $ B $ also the current is equal to $ I $ , in the same direction as in the previous case.
We know that a current carrying conductor carries a magnetic field around itself. This magnetic field, at a perpendicular distance $ r $ from the conductor is given by
 $ B = \dfrac{{{\mu _0}I}}{{2\pi r}} $
As both the value and the direction of the current are the same for both the observers, so they both observe the same magnetic field.
So, option A is correct and at the same time, options B and C are incorrect.
Since the conductor is electrically neutral, it carries no net charge. According to Coulomb's law, if net charge is zero, the electric field is also zero.
So, observers $ A $ and $ B $ do not observe any electric field.
This means that option D is correct.
Hence, options (A) and (D) are correct.

Note
We might argue that for the current carrying conductor given in the question, there is the involvement of the charge particles so it may generate an electric field. But, actually all the protons and electrons are distributed uniformly within the conductor. So, at every point electrical neutrality is maintained, because of which no electric field can be generated.