Question

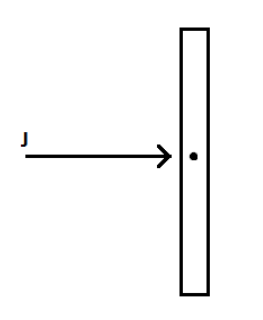
A straight bar of mass $15kg$ and length $2m$, at rest on a frictionless horizontal surface, receives an instantaneous impulse of $7Ns$ perpendicular to the bar. If the impulse is applied at the center of mass of the bar, the energy transferred is

     $A)\text{ }1.6J$
     $B)\text{ }1.9J$
     $C)\text{ 3}.8J$
     $D)\text{ 2}.5J$

Answer 1

Hint: This problem can be solved by using the fact that the impulse is equal to the momentum change of a body and the direct formula relating the change in momentum to the change in kinetic energy of the body.
Formula used:
$J=\Delta p$
$KE={{\dfrac{p}{2m}}^{2}}$

Complete answer:
The impulse $J$ upon a body is equal to the change in momentum $\Delta p$ of a body. That is,
$J=\Delta p$ --(1)
Also, the momentum $p$ of a body of mass $m$ is related to its kinetic energy $KE$ as
$KE={{\dfrac{p}{2m}}^{2}}$ --(2)
Now, let us analyze the question.
The mass of the bar is $m=15kg$.
The impulse given to the body is $J=7Ns$.
Therefore, let the momentum change of the rod be $\Delta p$.
Let the initial momentum and initial kinetic energy of the body just before the impulse be ${{p}_{i}}$ and $K{{E}_{i}}$ respectively.
Let the final momentum and final kinetic energy of the rod just after receiving the impulse be ${{p}_{f}}$ and $K{{E}_{f}}$ respectively.
Now, using (1), we get
$\Delta p=7Ns$ --(3)
Also, since the rod was at rest before the impulse, the initial momentum of the body is ${{p}_{i}}=0$.
Therefore, using (2), we get the corresponding initial kinetic energy as $K{{E}_{i}}=\dfrac{{{0}^{2}}}{2m}=0$. --(4)
Now,
$\Delta p={{p}_{f}}-{{p}_{i}}$
Putting (3) in the above equation, we get
$7={{p}_{f}}-0$
$\therefore {{p}_{f}}=7Ns$ --(5)
Therefore, the corresponding final kinetic energy of the rod will be
${{K}_{f}}=\dfrac{{{7}^{2}}}{2m}=\dfrac{49}{2\times 15}=\dfrac{49}{30}J$ [Using (5)] --(6)
Now, the energy transferred to the rod by the impulse will be nothing but
$\Delta KE=K{{E}_{f}}-K{{E}_{i}}$
Putting (4) and (6) in the above equation, we get
$\Delta KE=\dfrac{49}{30}-0=\dfrac{49}{30}\approx 1.6J$
Hence, the energy transferred by the impulse to the rod is $1.6J$.

Therefore, the correct option is $A)\text{ }1.6J$.

Note:
Students must note that impulse is nothing but the product of the force on a body and the time for which the force acts on the body. Impulse is usually the product of a large force and a small time period, that is, when a large force acts on a body for a small time (such as a cricket ball getting hit with a bat). Since, the force can be defined as the ratio of the momentum change of a body to the time in which the momentum changes, following that definition, the momentum change becomes equal to the product of the force and the time and hence, equal to the impulse on the body.