Question

A store sells two types of toys, A and B. The store owner pays \[Rs.{\rm{ }}8\] and \[Rs.{\rm{ }}14\] for each unit of toy A and toy B respectively. One unit of toy A yields a profit of \[Rs.{\rm{ 2}}\] while a unit of toy B yields a profit of \[Rs.{\rm{ 3}}\]. The store owner estimates that no more than \[2000\] toys will be sold every month and he does not plan to invest more than \[Rs.{\rm{ }}20,000\] in inventory of these toys. How many units of each type of toys should be stocked in order to maximize his monthly total profit?

Answer 1

Hint: When we assume the variables, a thing to remember is that they can not be negative as the number of items of any entity is always positive or zero, but it can never be negative. The same is the case with the price, total amount, et cetera; it has to always be positive or zero, but can never be negative. In the given question, we have to maximize the profit of the shopkeeper. So, we need to find the equations which represent the system of inequality, plot them on a graph, find the vertices of the obtained shape or curve and then solve under the restraints to find the maximum and that is going to be our answer.

Complete step by step answer:
Let the number of toys of \[A\] and \[B\] be \[x\] and \[y\] respectively. Either of the two cannot be negative, so:
\[x \ge 0\]
\[y \ge 0\]
Now, the store owner estimates that no more than \[2000\] toys will be sold, so:
\[x + y \le 2000\]
Given, the cost of \[A\] is \[Rs.{\rm{ 8}}\] and that of \[B\] is \[Rs.{\rm{ 14}}\].
Also, he says that he is not going to invest more than \[Rs.{\rm{ 20000}}\], so:
\[8x + 14y \le 20000\]
One unit of toy \[A\] earns a profit of \[Rs.{\rm{ }}2\] and that of \[B\] does \[Rs.{\rm{ }}3\], so,
\[P = 2x + 3y\]
So, we have to solve this equation, for finding the maximum profit.
\[ \Rightarrow x \ge 0\]
\[ \Rightarrow y \ge 0\]
\[ \Rightarrow x + y \le 2000\]
\[ \Rightarrow 8x + 14y \le 20000\]

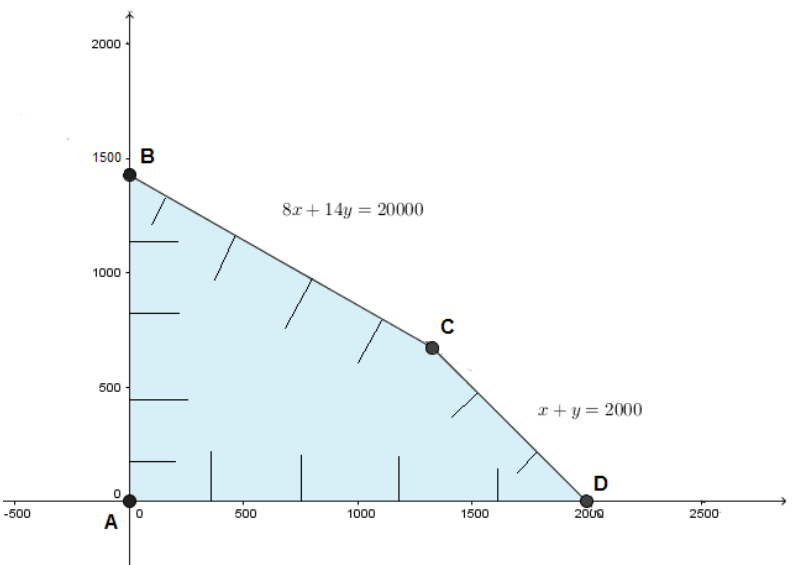
The vertices of the formed shape are:
\[ \Rightarrow A\left( {0,0} \right)\]
\[ \Rightarrow B\left( {0,1429} \right)\]
\[ \Rightarrow C\left( {1333,667} \right)\]
\[ \Rightarrow D\left( {2000,0} \right)\]

Calculating the profit at each vertex:
\[ \Rightarrow A\left( {0,0} \right) = 0\]
\[ \Rightarrow B\left( {0,1429} \right) = 4287\]
\[ \Rightarrow C\left( {1333,667} \right) = 4667\]
\[ \Rightarrow D\left( {2000,0} \right) = 4000\]
The maximum profit is at vertex \[C\].
So, the shopkeeper must sell \[1333\] units of toy \[A\] and \[667\] of toy \[B\].

Note: So, we saw that in solving questions like these, it is a cake walk if we just approach things systematically. In questions like these, we first find the equations which we are going to need to represent the system of inequality, plot the obtained system of the equations on a graph, find the vertices of the shape or curve we obtain by plotting the equations. Then, we just put in the values under the restraints and find the maximum or minimum (which depends upon what is being asked in the question) and then we are going to have the answer.