Question

A storage tank is in the form of a cube. When it is full of water, the volume of water is $156.25{{m}^{3}}$ If the present depth of water is $1.3m$. Find the volume of water already used from the tank.\[\]

Answer 1

Hint: We find the side of the cube sized storage tank by taking cube roots of both sides from the formula $V={{a}^{3}}$. We find volume of the cuboid space which emptied after the use of water with depth as difference between side and the new depth $1.3m$. Then we use the fact that $1{{m}^{3}}$of space will contain 1000 litre of water. \[\]

Complete step-by-step answer:
A cuboid is a three dimensional object with six rectangular faces joined by 8 vertices. It has three different types of sides called length, breadth and height denoted as $l,$$b$ and $h$ whose volume is given by$V=lbh$ . A cube is cuboid with condition $l=b=h$.\[\]

The amount space contained by a three dimensional object is measured by the quantity called volume. Let us take the length of the side of the cube as $a$. So the volume of a cube with is
\[V=a\times a\times a={{a}^{3}}..(1)\]
The amount of liquid with unit density is contained in the space by a cube of side of 1 cm is called 1 millilitre(ml). So the 1ml liquid is contained in $1cm\times 1cm\times 1cm=1c{{m}^{3}}$ of space. So So now we find how much liquid is contained in a cube with side 1 metre(m).\[\]
 The amount of space contained by a cube of 1m is
\[V=1m\times 1m\times 1m=100cm\times 100cm\times 100cm=100000c{{m}^{3}}\]
We know that 1000ml=1litre. $1c{{m}^{3}}$ of space contains 1 ml of liquid. So $1000000c{{m}^{3}}$ of space will be contained \[\text{1}000000\text{ml}=\dfrac{\text{1}000000}{1000}\text{=1}000\text{ litre}\] of liquid.
We find that a cube with side 1m or $1{{m}^{3}}$of space will contain 1000litre of liquid, in other words 1000litre of liquid will be contained by $1{{m}^{3}}$of space. \[\]

When the cubic tank is full the water will occupy all the volume. It is given that the volume of the cube is $156.25{{m}^{3}}$. We use equation (1) and put the given data
\[\begin{align}
  & V={{a}^{3}} \\
 & \Rightarrow {{a}^{3}}=156.25{{m}^{3}} \\
\end{align}\]
We take cube root both side and get
\[a={{\left( 156.25{{m}^{3}} \right)}^{\dfrac{1}{3}}}=2.5m\]

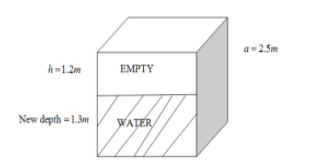
So the length of the side is 2.5. Now the depth of the water tank is $1.3m$. So the water used up empties the tank by decreasing the depth (or height)$h=2.5-1.3=1.2m$. The other two sides are $l=b=a=2.5m$. So the volume of the empties by using up the water is
\[ V=lbh=2.3\times 2.5\times 1.2=7.5{{m}^{3}}\]
We know r $1{{m}^{3}}$of space will contain 1000 litre of water. So the amount of water used up is $7.5\times 1000=7500$litre. \[\]

Note: We note that $1{{m}^{3}}$ of space will contain 1000 litre of liquid when the liquid is of unit density. We know that at normal temperature and without any impurity the density of water is $1gm/c{{m}^{3}}$, that means unit density .