Question

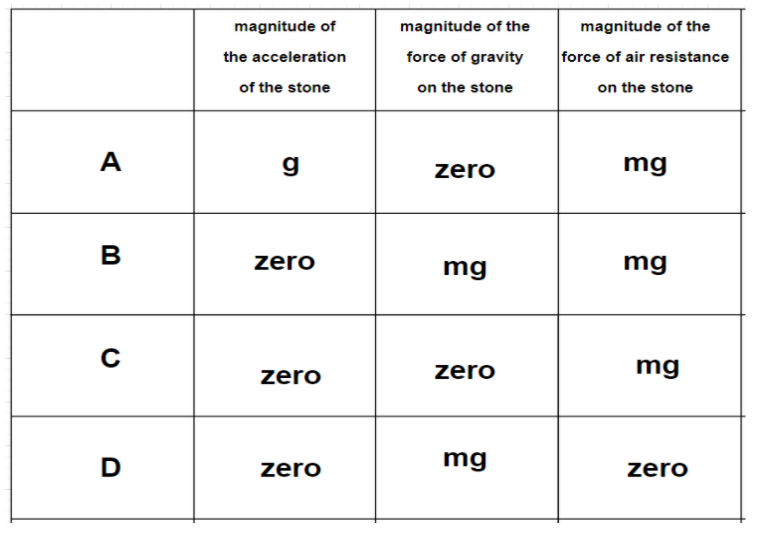
A stone of mass m is dropped from a tall building. There is significant air resistance. The acceleration of free fall is g. When the stone is falling at a constant (terminal) velocity, which information is correct?

Answer 1

Hint- Here, we will proceed by drawing a free body diagram of the stone at any instant. Then, we will apply the conditions of equilibrium on the since because the velocity of stone is constant.

Complete step-by-step solution -

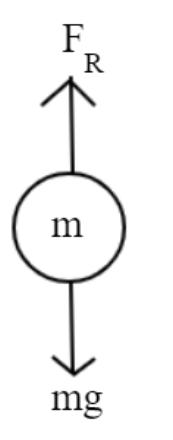
Let us suppose a stone of mass m which is dropped from a tall building. At any instant t, the free body diagram of the stone is shown in the figure. Due to the mass of the stone, weight or gravitational force acts on the stone which is of magnitude mg in the downward direction as shown where g is the acceleration of free fall.
Since, the air resistance needs to be considered because it is significant. There must be some force corresponding to the air resistance acting on the stone, let us assume it as ${{\text{F}}_{\text{R}}}$ as shown in the free body diagram.
When the stone is falling at a constant (terminal) velocity, the velocity with which this stone is falling downwards is constant. This means that no net acceleration is acting on the stone because net acceleration results in the increase or decrease in the velocity.
Therefore, the magnitude of acceleration acting on the stone is zero because the velocity with which stone is falling is constant.
Clearly, the gravitational force acting on the stone is mg (in downward direction). Therefore, the magnitude of the force of gravity on the stone is equal to mg.
Also, according to equilibrium conditions on a body, we can say that the total upward force acting on the body is equal to the total download force acting on the body.
By using above equilibrium conditions on the stone, we can write
${{\text{F}}_{\text{R}}} = {\text{mg}}$
i.e., the air resistance acting on the stone is equal to mg. The magnitude of the force of air resistance on the stone is mg.
Hence, option B is correct.

Note- Acceleration is defined as the rate of change of the velocity and is normally given as ${\text{a}} = \dfrac{{dv}}{{dt}}$ where v refers to the velocity of the body. Deceleration is basically a term used when the acceleration of the body is negative which refers that the magnitude of the velocity of the body will decrease.