Question

A stone of mass 6kg is revolved in a vertical circle of diameter 6m, such that its speed at a point is minimum. If the K.E at the same point is 250J, then the P.E. at this point is
A. 200J
B. 150J
C. 100J
D. 450J

Answer 1

Hint: The minimum velocity required for a particle to loop a loop while going in a vertical circle of radius r is $\sqrt {5gr} $. At the base, the P.E. of a body is zero and there will be only K.E. Use the law of conservation of mass to find the P.E. of the body at a point where the speed is minimum.

Complete step by step answer:

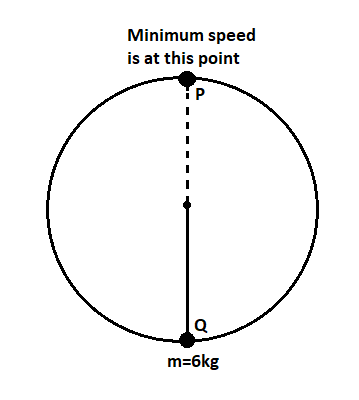
We are given that a stone of mass 6kg is revolved in a vertical circle of diameter 6m, such that its speed at a point is minimum. The point is P from the above figure. The K.E. at point P is 250J.
We have to find the Potential Energy at point P.
Q is the starting point for the stone. At Q, the potential energy is zero and only kinetic energy will be there.
The velocity of the stone at point Q is $\sqrt {5gr} $, where r is the radius and g is the acceleration due to gravity.

$
  r = \dfrac{d}{2} \\
  d = 6m \\
  \Rightarrow r = \dfrac{6}{2} = 3m \\
  r = 3m, g = 10m/{s^2} \\
$
$
  \Rightarrow v = \sqrt {5gr} \\
  \Rightarrow v = \sqrt {5 \times 10 \times 3} \\
  \Rightarrow v = \sqrt {150} = 5\sqrt 6 m/s \\
 $
By Law of conservation of Energy, total mechanical energy is equal to sum of kinetic energy and potential energy. The Mechanical energy at point P and Q must be equal as the energy can be neither created nor destroyed but can only be transformed.
$
  M.{E_p} = M.{E_q} \\
  \Rightarrow K.{E_p} + P.{E_p} = K.{E_q} + P.{E_q} \\
  P.{E_q} = 0 \\
  K.{E_p} = 250J \\
  \Rightarrow K.{E_q} + 0 = 250J + P.{E_p} \\
  K.{E_q} = \dfrac{1}{2}m{v^2} \\
  v = 5\sqrt 6 m/s \\
  \Rightarrow K.{E_q} = \dfrac{1}{2} \times 6 \times {\left( {5\sqrt 6 } \right)^2} \\
  \Rightarrow K.{E_q} = 3 \times 150 = 450J \\
  \Rightarrow 450J = 250J + P.{E_p} \\
  \Rightarrow P.{E_p} = 450 - 250 = 200J \\
 $
The potential energy at a point where the speed is minimum is 200J.
The correct answer is Option A.

Note:Kinetic energy of a system is the energy acquired by it by virtue of its motion whereas potential energy of a system is the energy acquired by it by virtue of its position. They are not the same. So do not confuse Kinetic Energy with Potential energy.