Question

A stone is projected up with a velocity of 4.9 m/s from the top of a tower and it reaches the ground after 3 s. Then the height of that tower is
a).4.9m
b).19.6m
c).9.8m
d).29.4m

Answer 1

Hint: We are given with velocity and time, and we need to find the distance. Lets first remember the equations of motion, we know that only two equations of motion have distance in them. But we are given with time and velocity and only one equation of motion is there in which we can put time, speed and velocity together and that is $S=ut+\dfrac{1}{2}a{{t}^{2}}$and we will be going to use this equation

Complete answer:

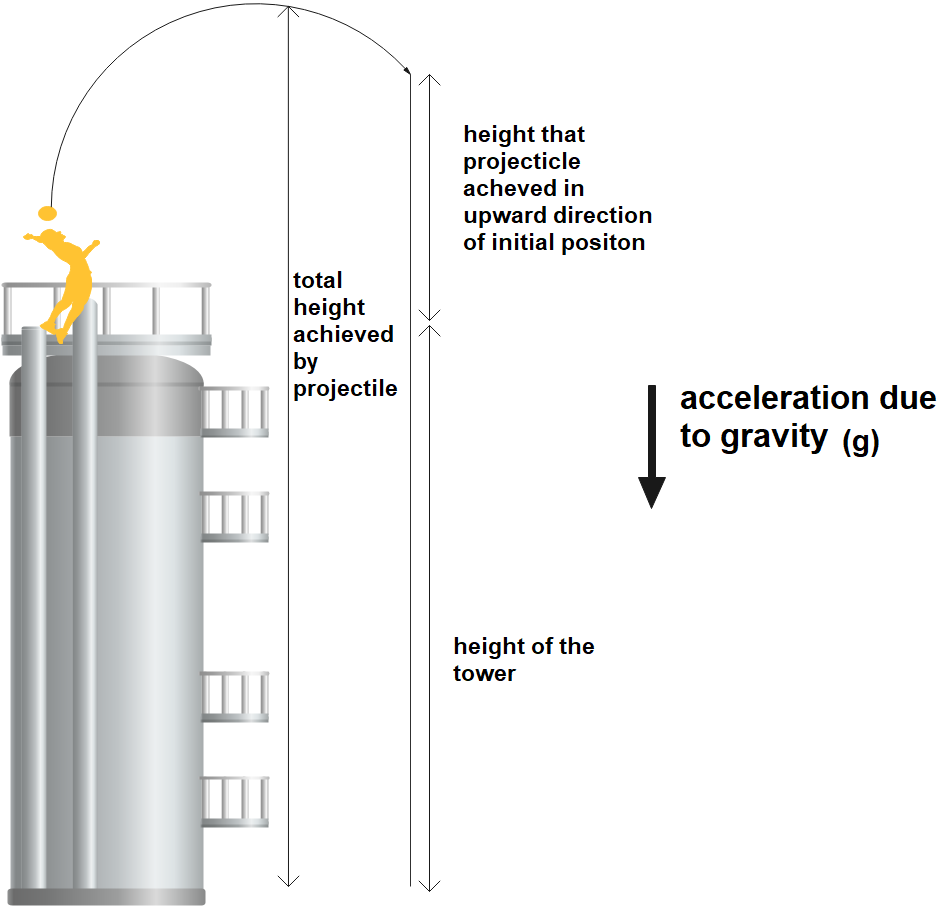
First step to solve any question is to write the given quantities. In this question we are given with the quantities as follows
u= 4.9m/s
Time(t) = 3 seconds
And we know that acceleration due to gravity(g) is 9.8m/s.
Since we are projecting the stone in upward direction, so we will take our upward direction as positive and downward direction as negative, and hence our acceleration due to gravity will be negative because it is acting downward and the projected velocity will be positive as it is acting upward. So, u= + 4.9m/s and g = -9.8m/s
First, we need to find the range, that the projectile would travel to attain a maximum height upward
For that we will use the formula ${{v}^{2}}-{{u}^{2}}=2as$
We would have final velocity (v) = 0 because at maximum height we have final velocity= 0 and s will be the distance that the projectile would travel to attain maximum height and according to figure this would be equal to (z).
Now put he value in above formula
$0-{{(4.9)}^{2}}=2\times 9.8\times s$
$s=\dfrac{24.01}{19.6}$
$s=1.225$
This is the height that the projectile will attain before start going in downward direction
And this same height it will cover to reach the height of tower, because it has gone in upward direction and to reach the height of tower it has to travel the same distance in downward direction.
Now we will find the total time taken to cover this total distance
We will use V= U+ at
$0=4.9+9.8t$
$t=0.5$ seconds
Now we will multiply this by 2 and hence we will get the total time it took to travel the total distance before reaching the height of the tower.
So t= 1 second
Since the projectile is reaching the ground in 3 seconds and it is taking 1 second to travel the distance it needed to again reach the height of the tower.
So remaining time (T) = 2 seconds
Now we will use the another equation of motion that is
${{S}_{T}}=uT+\dfrac{1}{2}a{{T}^{2}}$
Where ${{S}_{T}}$ is the height of the tower.
Put the values in the given equation
We will have initial velocity as 0, hence u=0
${{S}_{T}}=0+\dfrac{1}{2}(9.8){{(2)}^{2}}$
${{S}_{T}}=19.6$m

Hence Option (B) is the correct answer for this question.

Note:
When we through a projectile it will go in upward direction and the gravity will push it in downward direction, so the projectile will travel in upward direction until it reaches in a situation to stop and when its final velocity will become zero it will start acceleration in downward direction, because of gravity. It will travel the same distance in downward direction, which it travelled in upward direction to again reach its initial height from where it was thrown and that height is the height of the tower.