Question

A stone is dropped from a height of 45 m. What will be the distance travelled by it during the last second of its motion?
$\text{A}\text{. 30 m}$
$\text{B}\text{. 25 m}$
$\text{C}\text{. 15 m}$
$\text{D}\text{. 05 m}$

Answer 1

Hint: When an object is dropped from a height, it moves under the sole influence of gravitational force due to earth. This motion of objects under the influence of gravity is known as free fall. The object accelerates with a constant acceleration due to gravity.

Complete step by step answer:

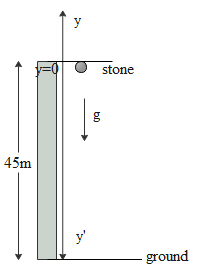
We know that the vertical distance covered by a freely falling body in time $t$ is given by
$h=ut-\dfrac{1}{2}g{{t}^{2}}$
Where
$h=$ Vertical distance covered
$u=$ Initial velocity
$t=$ Time period
$g=$ Acceleration due to gravity $\approx 10m{{s}^{-2}}$
Here the object is dropped so the initial velocity of the object is zero. Therefore the equation becomes
$h=-\dfrac{1}{2}g{{t}^{2}}$
Negative sign is used because we have assumed the origin at height $45m$ from where stone is dropped.
Using this equation, we can calculate the total time taken by the object to reach ground. Let us substitute the corresponding values:
$-45=-\dfrac{1}{2}\times 10\times {{t}^{2}}$
On rearranging we get
${{t}^{2}}=9{{s}^{2}}$
Or $t=3\text{ s}$
The distance travelled by stone can be calculated as
$\Delta {{h}_{t-1,t}}={{h}_{t}}-{{h}_{t-1}}$
Or $\Delta {{h}_{t-1,t}}=-\dfrac{1}{2}g[{{t}^{2}}-{{(t-1)}^{2}}]$
On substituting the value of $t=3s$ we get
$\Delta {{h}_{t-1,t}}=-\dfrac{1}{2}\times 10[{{3}^{2}}-{{2}^{2}}]$
$=-25m$
Negative sign here shows that the stone has fallen downward by 25 meter in the last second.

So, the correct answer is “Option B”.

Additional Information: This problem can also be solved by another method. For that, we will need to calculate velocities of stone at ${{t}^{th}}$ and ${{(t-1)}^{th}}$ second. Then we can use equation
${{v}^{2}}-{{u}^{2}}=2gh$. To calculate distance travelled at the last second.

Note: In such types of questions, sometimes students forget to consider the initial velocity of the object during free fall as zero. Students should take care of it. Sometimes students may also get confused and may calculate the distance covered by the object in the first second of the free fall.