Question

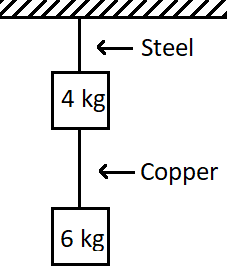
A steel wire (original length $ = 2m $ , diameter $ = 1mm $ ) and a copper wire (original length $ = 1m $ , diameter $ = 2mm $ ) are loaded as shown in the figure. Find the ratio of extension of steel wire to that of copper wire. Given, Young’s modulus of steel $ = 2 \times {10^{11}}N{m^{ - 2}} $ and that of copper is $ {10^{11}}N{m^{ - 2}} $ .

(A) $ \dfrac{{10}}{3} $
(B) $ 5 $
(C) $ \dfrac{{20}}{3} $
(D) $ \dfrac{{14}}{3} $

Answer 1

Hint We need to find the elongation of the steel wire by using the formula for the Young’s modulus, where we can consider Young’s modulus for steel wire as $ 2 \times {10^{11}}N{m^{ - 2}} $ and the force on the wire is $ 10Kg $ . Similarly we need to find the elongation of the copper wire by using the formula for the Young’s modulus, where we can consider Young’s modulus for copper wire as $ {10^{11}}N{m^{ - 2}} $ and the force on the wire is $ 6Kg $ .Then we need to find the ratio of the extension in lengths.

Formula Used:
In this solution we will be using the following formula,
 $\Rightarrow Y = \dfrac{{\left( {{F \mathord{\left/
 {{F A}} \right.
 } A}} \right)}}{{\left( {{{\Delta L} \mathord{\left/
 {{{\Delta L} L}} \right.
 } L}} \right)}} $
where $ Y $ is Young’s modulus, $ F $ is the force on the wire, $ A $ is the area of cross-section of the wire, $ L $ is the length of the wire and $ \Delta L $ is the elongation in length of the wire.

Complete step by step answer
In the figure we can see that the steel wire is given of a length of $ 2m $ and $ 1mm $ in diameter. Now the weight that is suspended from the brass wire is $ 10Kg $ . So the force that is acting on the wire is due to this weight.
Now the diameter of the wire is $ 1mm $ , so the radius is, $ r = \dfrac{1}{2}mm = 0.5mm $ . We can write the radius in meters as, $ r = 0.5mm = 5 \times {10^{ - 4}}m $ .
So using this radius of the steel wire we can calculate its area of cross-section. Hence we get the area of cross-section of the wire as,
 $\Rightarrow A = \pi {r^2} $
Substituting the value we get
 $\Rightarrow A = \pi {\left( {5 \times {{10}^{ - 4}}} \right)^2} $
That gives us on calculating the area of cross-section as,
 $\Rightarrow A = 7.85 \times {10^{ - 7}}{m^2} $
The Young’s modulus of the brass wire is given by the formula,
 $\Rightarrow Y = \dfrac{{\left( {{F \mathord{\left/
 {{F A}} \right.
 } A}} \right)}}{{\left( {{{\Delta L} \mathord{\left/
 {{{\Delta L} L}} \right.
 } L}} \right)}} $
It can be written in a simplified way as
 $\Rightarrow Y = \dfrac{{F \times L}}{{A \times \Delta L}} $
From here we can write the equation in form of the elongation in length as,
 $\Rightarrow \Delta L = \dfrac{{F \times L}}{{A \times Y}} $
Now the given length of the wire is $ L = 2m $ and the force on the wire is $ F = 10gN = 10 \times 9.8N $ , which gives us a force of $ F = 98N $ . And the Young’s modulus for steel is given by, $ Y = 2 \times {10^{11}}N{m^{ - 2}} $ . So substituting all these values in the equation for the elongation in length we get
 $\Rightarrow \Delta L = \dfrac{{98 \times 2}}{{7.85 \times {{10}^{ - 7}} \times 2 \times {{10}^{11}}}} $
On doing the calculations in the numerator and the denominator we get,
 $\Rightarrow \Delta L = \dfrac{{196}}{{1.57 \times {{10}^5}}} $
On doing the division, we obtain the value of the elongation in length as,
 $\Rightarrow \Delta L = 1.2 \times {10^{ - 3}}m $
Similarly, for the copper wire, the diameter of the wire is $ 2mm $ , so the radius is, $ r = \dfrac{2}{2}mm = 1mm $ . We can write the radius in meters as, $ r = 1mm = {10^{ - 3}}m $ .
So using this radius of the steel wire we can calculate its area of cross-section. Hence we get the area of cross-section of the wire as,
 $\Rightarrow A = \pi {r^2} $
Substituting the value we get
 $\Rightarrow A = \pi {\left( {{{10}^{ - 3}}} \right)^2} $
That gives us on calculating the area of cross-section as,
 $\Rightarrow A = 3.14 \times {10^{ - 6}}{m^2} $
We are given the given length of the wire is $ L = 1m $ and the force on the wire is $ F = 6gN = 6 \times 9.8N $ , which gives us a force of $ F = 58.8N $ . And the Young’s modulus for copper is given by, $ Y = {10^{11}}N{m^{ - 2}} $ . So substituting all these values in the equation for the elongation in length we get
 $\Rightarrow \Delta L = \dfrac{{58.8 \times 1}}{{3.14 \times {{10}^{ - 6}} \times {{10}^{11}}}} $
On doing the calculations in the numerator and the denominator we get,
 $\Rightarrow \Delta L = \dfrac{{58.8}}{{3.14 \times {{10}^5}}} $
On doing the division, we obtain the value of the elongation in length as,
 $\Rightarrow \Delta L = 1.87 \times {10^{ - 4}}m $
So taking the ratio we get, $ \dfrac{{\Delta {L_s}}}{{\Delta {L_c}}} = \dfrac{{1.2 \times {{10}^{ - 3}}}}{{1.87 \times {{10}^{ - 4}}}} $
On calculating we have,
 $\Rightarrow \dfrac{{\Delta {L_s}}}{{\Delta {L_c}}} = 6.5 $
This is equivalent to $ \dfrac{{\Delta {L_s}}}{{\Delta {L_c}}} = \dfrac{{20}}{3} $
So the correct answer is option C.

Note
The Young’s modulus of any substance is its ability to undergo tension or compression in the direction of its length. It is its ability to withstand a change in length. It is given numerically by the ratio of the longitudinal stress to the strain of the wire.