
A steamer going downstream in a river, covers the distance between 2 towns in 15 hours. Coming back upstream, it covers this distance in 20 hours. The speed of water is 3 $\dfrac{km}{hr}$. Find the distance between two towns.
(a) 360km
(b) 220km
(c) 180km
(d) 120km
Answer
626.7k+ views
Hint: Downstream means stream and streamer are moving in the same direction and upstream means stream and streamer are moving in the opposite direction. So, suppose the speed of the streamer in still water as a variable and hence find the speed of streamer in downstream and upstream with the help of relation $\text{Speed}\ \text{=}\ \dfrac{\text{Distance}}{\text{Time}}$. Now form two equations in terms of distance and speed of streamer and hence solve it further.
Complete step-by-step answer:
Let the distance between both the towns is ‘d’km and the speed of streamers in still water is ‘u’ $\dfrac{km}{hr}$.
Now we know that streamer and flow of water (streamer) are in the opposite direction and downstream means that the direction of stream (water flow) and streamer are the same.
It means speed of streamer in downstream direction is the sum of speed of stream and streamer in still water and speed of streamer in upstream direction is difference of speed of streamer in still direction and speed of stream.
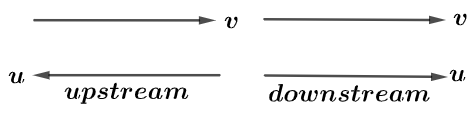
Where u is the speed of streamer in still water and v is the speed of stream.
Hence, the speed of stream in downstream direction is $u+v$.
Speed of stream in upstream direction is $u-v$.
Now, coming to the question we have the speed of water as 3$\dfrac{km}{hr}$. And time taken by streamers downstream are 15 hours and 20 hours respectively.
So, we know the relation among speed, distance and time as
$\text{Speed}\ \text{=}\ \dfrac{\text{Distance}}{\text{Time}}$ ………………………………………………………………………………………………(i)
So, for upstream, we have
Speed of streamer $=\ u+v$
Time taken to cover distance between towns $=\ 15\ \text{hours}$
Distance between towns $=\ d\ \text{km}$
So, we get
$u+v\ =\ \dfrac{d}{15}$
Put $v\ =\ 3\ \dfrac{km}{hr}$ as the speed of water is 3 $\dfrac{km}{hr}$. from the problem. Hence, we get
$u+3\ =\ \dfrac{d}{15}$
$\Rightarrow u\ =\ \dfrac{d}{15}-3$ ……………………………………………………………………………………….(ii)
And, for upstream, we have
Speed of streamer $=\ u-v$
Time taken to cover the distance ‘d’ $=\ 20\ \text{hours}$
Distance between both towns $=\ d\ \text{km}$
So, we get from the equation (i) as
$u-v\ =\ \dfrac{d}{20}$
Now, put \[v\ =\ 3\ \dfrac{km}{hr}\] to the above equation so, we get
\[u-\ 3\ =\ \dfrac{d}{20}\]
\[\Rightarrow u\ =\ \dfrac{d}{20}+3\] …………………………………………………………………………………(iii)
Now, we can equate the value of ‘u’ from the equation (ii) and (iii) as both are representing the same value. Hence, we get
\[\dfrac{d}{15}-3\ =\ \dfrac{d}{20}+3\]
\[\dfrac{d}{15}-\dfrac{d}{20}\ =\ 3+3\]
Take L.C.M. of denominators of fractions of L.H.S. to solve the expression; so, we get
\[\dfrac{4d-3d}{60}\ =\ 6\]
\[\dfrac{d}{60}\ =\ 6\]
\[d\ =\ 360\ \text{km}\]
Hence, the distance between the two towns is 360 km.
So, Answer (a) is correct.
Note: Terms ‘downstream’ and ‘upstream’ should be clear to solve these types of questions. Don’t get confused with the word stream, it is used for the speed of water flow.
One may take the velocities of streamers as $v-u$ and $v+u$ as well, and if one finds the ‘u’ as negative value, don’t get confused. Negative sign represents the direction only.
Don’t get confused with the relation of $\text{Speed}\ \text{=}\ \dfrac{\text{Distance}}{\text{Time}}$ . Students get confuse with these relation as well and may apply formula as $\text{Time}\ \text{=}\ \dfrac{\text{Speed}}{\text{Time}}$ or $\text{Time}\ \text{=}\ \text{Distance}\times \text{Speed}$ which are wrong. So, be clear with the relation speed distance and time.
Complete step-by-step answer:
Let the distance between both the towns is ‘d’km and the speed of streamers in still water is ‘u’ $\dfrac{km}{hr}$.
Now we know that streamer and flow of water (streamer) are in the opposite direction and downstream means that the direction of stream (water flow) and streamer are the same.
It means speed of streamer in downstream direction is the sum of speed of stream and streamer in still water and speed of streamer in upstream direction is difference of speed of streamer in still direction and speed of stream.
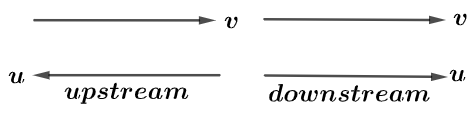
Where u is the speed of streamer in still water and v is the speed of stream.
Hence, the speed of stream in downstream direction is $u+v$.
Speed of stream in upstream direction is $u-v$.
Now, coming to the question we have the speed of water as 3$\dfrac{km}{hr}$. And time taken by streamers downstream are 15 hours and 20 hours respectively.
So, we know the relation among speed, distance and time as
$\text{Speed}\ \text{=}\ \dfrac{\text{Distance}}{\text{Time}}$ ………………………………………………………………………………………………(i)
So, for upstream, we have
Speed of streamer $=\ u+v$
Time taken to cover distance between towns $=\ 15\ \text{hours}$
Distance between towns $=\ d\ \text{km}$
So, we get
$u+v\ =\ \dfrac{d}{15}$
Put $v\ =\ 3\ \dfrac{km}{hr}$ as the speed of water is 3 $\dfrac{km}{hr}$. from the problem. Hence, we get
$u+3\ =\ \dfrac{d}{15}$
$\Rightarrow u\ =\ \dfrac{d}{15}-3$ ……………………………………………………………………………………….(ii)
And, for upstream, we have
Speed of streamer $=\ u-v$
Time taken to cover the distance ‘d’ $=\ 20\ \text{hours}$
Distance between both towns $=\ d\ \text{km}$
So, we get from the equation (i) as
$u-v\ =\ \dfrac{d}{20}$
Now, put \[v\ =\ 3\ \dfrac{km}{hr}\] to the above equation so, we get
\[u-\ 3\ =\ \dfrac{d}{20}\]
\[\Rightarrow u\ =\ \dfrac{d}{20}+3\] …………………………………………………………………………………(iii)
Now, we can equate the value of ‘u’ from the equation (ii) and (iii) as both are representing the same value. Hence, we get
\[\dfrac{d}{15}-3\ =\ \dfrac{d}{20}+3\]
\[\dfrac{d}{15}-\dfrac{d}{20}\ =\ 3+3\]
Take L.C.M. of denominators of fractions of L.H.S. to solve the expression; so, we get
\[\dfrac{4d-3d}{60}\ =\ 6\]
\[\dfrac{d}{60}\ =\ 6\]
\[d\ =\ 360\ \text{km}\]
Hence, the distance between the two towns is 360 km.
So, Answer (a) is correct.
Note: Terms ‘downstream’ and ‘upstream’ should be clear to solve these types of questions. Don’t get confused with the word stream, it is used for the speed of water flow.
One may take the velocities of streamers as $v-u$ and $v+u$ as well, and if one finds the ‘u’ as negative value, don’t get confused. Negative sign represents the direction only.
Don’t get confused with the relation of $\text{Speed}\ \text{=}\ \dfrac{\text{Distance}}{\text{Time}}$ . Students get confuse with these relation as well and may apply formula as $\text{Time}\ \text{=}\ \dfrac{\text{Speed}}{\text{Time}}$ or $\text{Time}\ \text{=}\ \text{Distance}\times \text{Speed}$ which are wrong. So, be clear with the relation speed distance and time.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

State and prove Bernoullis theorem class 11 physics CBSE

Actinoid contraction is more than lanthanoid contraction class 11 chemistry CBSE

The transition element that has lowest enthalpy of class 11 chemistry CBSE

Can anyone list 10 advantages and disadvantages of friction

State the laws of reflection of light




