Question

A steamer goes downstream and covers the distance between two ports in 4 hours while it covers the same distance upstream in 5 hours. If the speed of the stream is 2km/hr, find the speed of the steamer in still water.
A.12 km/hr
B.31 km/hr
C.18 km/hr
D.15 km/hr

Answer 1

Hint: Downstream means stream and streamer are travelling in the same direction while upstream means stream and steamer are moving in the opposite direction. Suppose the speed of the streamer as a variable and use the relation among speed, distance and time which can be given as
$\text{Speed}=\dfrac{\text{Distance}}{\text{Time}}$

Complete step-by-step answer:

Let the speed of the streamer in the still water be ‘u’ km/hr in the still water. Now, we know the meaning of upstream direction that streamer and flow of water (stream) are in opposite directions and downstream means that direction of stream (water flow) and streamer are the same. It means speed of streamer in downstream direction is the sum of speed of stream and streamer in still direction and speed of stream.

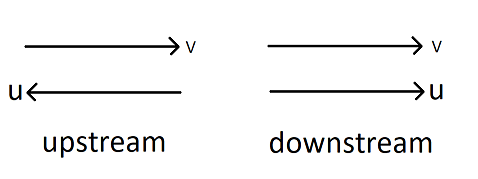
Where u is the speed of a streamer in still water. And v is the speed of the stream. Hence, the speed of stream in downstream direction is u + v. Speed of stream in upstream direction is u – v.
Now, coming to the question, it is given that streamer covers a distance in 4 hours with downstream direction and same distance in 5 hours with upstream direction and we need to determine the speed of streamer in still water if speed of stream (water flow) is 2km/hr. Let the distance covered in one direction is d. Now, we know the relation among speed, distance and time is given as
$\text{Speed}=\dfrac{\text{Distance}}{\text{Time}}................\left( i \right)$
Now, for downstream direction, we have
Speed = u + v
Distance = d
Time = 4hours
So, we get from equation (i) as
$u+v=\dfrac{d}{4}$
Now, put speed of stream = v =2km/hr
$\dfrac{u+2}{1}=\dfrac{d}{4}$
On cross-multiplication the above equation, we get
4u + 8 = d or
d = 4u + 8…………………(ii)
Similarly, for upstream direction, we have
Speed = u – v
Distance = d
Time = 5 hours
Hence, we can get from equation (i) as
$u-v=\dfrac{d}{5}$
Put v = 2km/hr
$\dfrac{u-2}{1}=\dfrac{d}{5}$
On cross multiplying the above equation, we get
5u – 10 = d or
d = 5u – 10……………..(iii)
Now, we can equate values of ‘d’ from equation (ii) and (iii) as both values of ‘d’ are representing the same value. So, we get
4u + 8 = 5u – 10
8 + 10 = 5u – 4v
u = 18km/hr
Hence, the speed of streamers in still water is 18km/hr.
So, option (c) is correct.

Note: Terms ‘downstream’ and ‘upstream’ should be clear to solve these types of questions. Don’t get confused with the word stream, it is used for the speed of water flow.
One may take the velocities of streamers as v – u and v + u as well, and if one finds them as a negative value, don’t get confused. Negative signs represent the direction only. Don’t get confused with the relation $\text{Speed}=\dfrac{\text{Distance}}{\text{Time}}$ . Students get confuse with this relation as well and may apply formula as $\text{Time}=\dfrac{\text{Speed}}{\text{Time}}$ or $\text{time}=\text{distance}\times \text{speed}$ which are wrong. So, be clear with the relation of speed, distance and time.