Question

A statue$8$ meters high standing on the top a tower $64$ meters high, on the bank
of a river, subtends at a point A on the opposite bank, directly facing the tower, the same
angle as subtended at the same point A by man of height $2$ meters standing at the base of
The tower that then extends the breadth of the river is ${\rm{16}}\sqrt {\rm{6}} $meters.
C. True
D. False

Answer 1

Hint: Use the trigonometric ratio of tangent, to relate the sides. Use the formula of tangent of
sum of two angles.
Complete step-by-step answer:
Here, it is given that,
The height of the tower is $64$ meters.
The height of the statue which is standing on the top of the tower is$8$meters. The height of the man is $2$ meters.
For the given problem, a diagram will be more helpful which is given below:

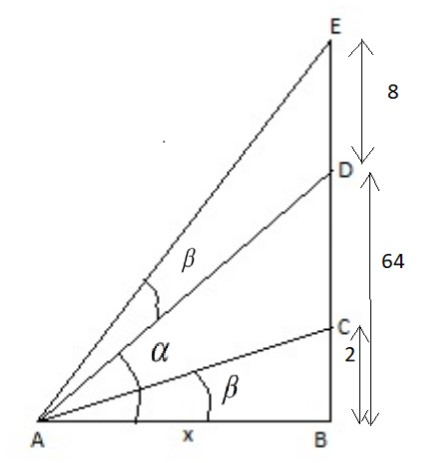
In the above diagram:
AB $\left( x \right)$ = Breadth of the river

BC = Height of the man.
BD = Height of the tower.
DE = Height of the statue.
$\alpha $ is the angle DAB and $\beta $ is the angle DAE and BAC.
$\beta $ is the angle subtended by the man as well as by the statue at point A, which is a
pointy along the other bank of the river, whose breadth needs to be calculated.
In the $\Delta ABC$, apply the trigonometric ratio of a triangle, you have:
$\begin{array}{c}\tan \beta = \dfrac{{BC}}{{AB}}\\ = \dfrac{2}{x}\end{array}$
…… (1)
In the $\Delta ABD$, apply the trigonometric ratio of a triangle, you have:
$\begin{array}{c}\tan \alpha = \dfrac{{BD}}{{AB}}\\ = \dfrac{{64}}{x}\end{array}$

…… (2)

In the $\Delta ABE$, apply the trigonometric ratio of a triangle, you have:
$\begin{array}{c}\tan \left( {\alpha + \beta } \right) = \dfrac{{BE}}{{AB}}\\ = \dfrac{{64
+ 8}}{x}\\ = \dfrac{{72}}{x}\end{array}$ …… (3)
Recall the formula:
$\tan \left( {\alpha + \beta } \right) = \dfrac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan
\beta }}$ …… (4)
Substitute the values from equations (1), (2) and (3) in the formula (4), you get,
$\begin{array}{l}\tan \left( {\alpha + \beta } \right) = \dfrac{{\tan \alpha + \tan \beta }}{{1
- \tan \alpha \tan \beta }}\\ \Rightarrow \dfrac{{72}}{x} = \dfrac{{\dfrac{{64}}{x} +
\dfrac{2}{x}}}{{1 - \dfrac{{64}}{x} \times \dfrac{2}{x}}}\\ \Rightarrow \dfrac{{72}}{x}
= \dfrac{{\dfrac{{64 + 2}}{x}}}{{1 - \dfrac{{2 \times 64}}{{{x^2}}}}}\\ \Rightarrow
\dfrac{{72}}{x} = \dfrac{{\dfrac{{66}}{x}}}{{1 - \dfrac{{128}}{{{x^2}}}}}\\
\Rightarrow \dfrac{{72}}{x} = \dfrac{{\dfrac{{66}}{x}}}{{\dfrac{{{x^2} -
128}}{{{x^2}}}}}\\ \Rightarrow \dfrac{{72}}{x} = \dfrac{{66}}{{\not x}} \times
\dfrac{{{x^{\not 2}}}}{{{x^2} - 128}}\\ \Rightarrow \dfrac{{72}}{x} =
\dfrac{{66x}}{{{x^2} - 128}}\end{array}$
Now, apply cross-multiplication,
$\begin{array}{l} \Rightarrow 72 \times \left( {{x^2} - 128} \right) = 66x \times x\\
\Rightarrow 72{x^2} - 9216 = 66{x^2}\\ \Rightarrow 72{x^2} - 66{x^2} = 9216\\
\Rightarrow 6{x^2} = 9216\\ \Rightarrow {x^2} = \dfrac{{9216}}{6}\\ \Rightarrow {x^2} =
1536\\ \Rightarrow {x^2} = 6 \times 16 \times 16\\ \Rightarrow x = \sqrt {6 \times 16 \times
16} \\ \Rightarrow x = 16\sqrt 6 \,{\rm{m}}\end{array}$

Hence, the breadth of the river is $16\sqrt 6 \;{\rm{m}}$.

So, it is true.

Note: In the given problem, the breadth of the river is to be calculated. Find the trigonometric
ratios for all the angles. Equate all the ratios to find the breadth of the river.