Question

A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is ${60^0}$ and from the same point the angle of elevation of the top of the pedestal is ${45^0}$. Find the height of the pedestal.

Answer 1

Hint: Here, we will proceed by drawing the figure according to the problem statement and then, using the definition of the tangent trigonometric function i.e., $\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$ in both the right angled triangles formed i.e., ABD and ABC.

Complete step-by-step answer:
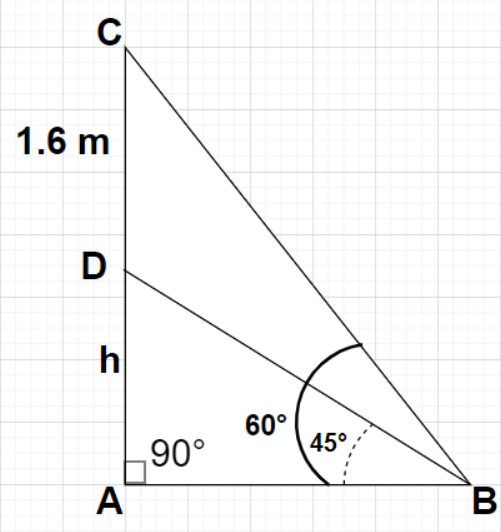
Let the height of the pedestal be h m as shown in the figure
Given, Height of the statue, CD = 1.6 m
Angle of elevation of the top of the statue from point B, $\angle {\text{ABC}} = {60^0}$
Angle of elevation of the top of the pedestal from point B, $\angle {\text{ABD}} = {45^0}$
According to the definition of tangent trigonometric function in any right angled triangle,
$\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}{\text{ }} \to (1{\text{)}}$
Using formula given by equation (1) in right angled triangle ABC, we have
$
   \Rightarrow \tan \left( {\angle {\text{ABC}}} \right) = \dfrac{{{\text{AC}}}}{{{\text{AB}}}} \\
   \Rightarrow \tan \left( {\angle {\text{ABC}}} \right) = \dfrac{{{\text{AD}} + {\text{DC}}}}{{{\text{AB}}}} \\
   \Rightarrow \tan \left( {{{60}^0}} \right) = \dfrac{{h + 1.6}}{{{\text{AB}}}} \\
 $
According to the general trigonometric table, $\tan \left( {{{60}^0}} \right) = \sqrt 3 $
$
   \Rightarrow \sqrt 3 = \dfrac{{h + 1.6}}{{{\text{AB}}}} \\
   \Rightarrow {\text{AB}} = \dfrac{{h + 1.6}}{{\sqrt 3 }}{\text{ }} \to {\text{(2)}} \\
 $
Using formula given by equation (1) in right angled triangle ABD, we have
$
   \Rightarrow \tan \left( {\angle {\text{ABD}}} \right) = \dfrac{{{\text{AD}}}}{{{\text{AB}}}} \\
   \Rightarrow \tan \left( {{{45}^0}} \right) = \dfrac{h}{{{\text{AB}}}} \\
 $
According to the general trigonometric table, $\tan \left( {{{45}^0}} \right) = 1$
$
   \Rightarrow 1 = \dfrac{h}{{{\text{AB}}}} \\
   \Rightarrow {\text{AB}} = h{\text{ }} \to {\text{(3)}} \\
 $
Clearly, the LHS of both the equations (2) and (3) are same which means that the RHS of these equations will also be equal
i.e., \[
   \Rightarrow \dfrac{{h + 1.6}}{{\sqrt 3 }} = h \\
   \Rightarrow h + 1.6 = \sqrt 3 h \\
   \Rightarrow \sqrt 3 h - h = 1.6 \\
   \Rightarrow h\left( {\sqrt 3 - 1} \right) = 1.6 \\
   \Rightarrow h = \dfrac{{1.6}}{{\left( {\sqrt 3 - 1} \right)}} = \dfrac{{1.6}}{{\left( {1.732 - 1} \right)}} = \dfrac{{1.6}}{{0.732}} \\
   \Rightarrow h = 2.186{\text{ m}} \\
 \]
Therefore, the height of the pedestal is 2.186 metres.

Note- In any right angled triangle, the side opposite the right angle is hypotenuse, the side opposite to the considered angle is perpendicular and the remaining side is base. In right angled triangle ABC, BC is the hypotenuse, AC is the perpendicular and AB is the base when the considered angle is $\angle {\text{ABC}}$.