Question

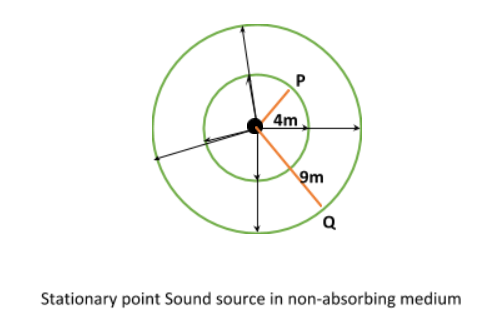
A stationary point source of sound emits sound uniformly in all directions in a non-absorbing medium. Two points P and Q are at a distance of 4m and 9m respectively from the source. The ratio of amplitudes of the waves at P and Q if
A. \[\dfrac{3}{2}\]
B. \[\dfrac{4}{9}\]
C. \[\dfrac{4}{9}\]
D. \[\dfrac{9}{4}\]

Answer 1

Hint:To solve the given problem first we have to figure out how the intensity of the point source varies with the distance and then we will use the expression that relates intensity and amplitude of the sound source in order to establish a relation between amplitude and the distance. We will take the formula:
\[I = k{A^2}\] or
\[A = \sqrt {\dfrac{I}{k}} \], where \[I\], \[k\] and \[A\] are Intensity, proportionality constant, and amplitude of the sound source.

Complete step-by-step answer:
 To get the required ratio of amplitude we are using the formula of Intensity as:
\[I = \dfrac{{Energy}}{{Area \times time}}\]
\[ \Rightarrow I \propto \dfrac{1}{{Area}}\]…………………….. (i)
Since, \[A \propto {\left( I \right)^{\dfrac{1}{2}}}\]……………………(ii)
Comparing both eqn (i) and eqn (ii), we get
\[A \propto {\left( {\dfrac{1}{{Area}}} \right)^{\dfrac{1}{2}}}\]
\[ \Rightarrow A = C{\left( {\dfrac{1}{{Area}}} \right)^{\dfrac{1}{2}}}\]………………………….(iv)
Now, on moving toward the point stationary source of sound in the non-absorbing medium
As the sound wave is propagating in all directions so we use two 3-dimensional spheres of radii 4m and 9m to get the amplitudes at point 4m and 9m respectively.
Substitute the surface areas of small and large spheres in eqn (iv),

We get,
Amplitude\[({A_1}) = C{\left( {\dfrac{1}{{Are{a_1}}}} \right)^{\dfrac{1}{2}}}\]………. (v)
Amplitude \[({A_2}) = C{\left( {\dfrac{1}{{Are{a_2}}}} \right)^{\dfrac{1}{2}}}\]……… (vi),
(Where C is a proportionality constant.)
Divide eqn (v) by eqn (vi), we get:
\[\dfrac{{{A_1}}}{{{A_2}}} = {\left( {\dfrac{{Are{a_2}}}{{Are{a_1}}}} \right)^{\dfrac{1}{2}}}\]…………….(vii)
Substituting-(\[Are{a_1} = 4\pi {r_1}^2\] and \[Are{a_2} = 4\pi {r_2}^2\]) where we take \[{r_1} = 4m\] and \[{r_2} = 9m\].
We have
\[\dfrac{{{A_1}}}{{{A_2}}} = {\left( {\dfrac{{{r_2}^2}}{{{r_1}^2}}} \right)^{\dfrac{1}{2}}} = \left( {\dfrac{{{r_2}}}{{{r_1}}}} \right)\]
\[ \Rightarrow \dfrac{{{A_1}}}{{{A_2}}} = \left( {\dfrac{9}{4}} \right)\]
Hence, the correct answer is (D).

Note: In order to find these kinds of formula-based questions the key is to remember the various fact-based short-formula and their implementation while solving the tricky numerical problems. One should also remember that to obtain the final expression for the ratio of amplitude is derived under consideration of stationary point source it may vary for sound sources like linear source or source at infinite distance.