Question

A stationary observer receives sound from two identical tuning forks, one of which approaches and the other one recedes with the same speed (much less than the speed of sound). The observer hears 2 beats/sec. The oscillation frequency of each tuning fork is ${{\nu }_{0}}=1400Hz$ and the velocity of sound in air is 350m/s. The speed of each tuning fork is close to:
A. $1m/s$
B. $\dfrac{1}{8}m/s$
C. $\dfrac{1}{2}m/s$
D. $\dfrac{1}{4}m/s$

Answer 1

Hint: We have two tuning forks with the same frequency moving in opposite directions, one towards the observer and other away from the observer. We are also given the beats per second heard by the observer. First we solve for the two frequencies heard by the observer and then solve for beats. Thus we get the speed of both sources.

Formula used:
Beat frequency,
${{f}_{b}}=\left| {{f}_{1}}-{{f}_{2}} \right|$
${{f}_{1}}=\left( \dfrac{v}{v-{{v}_{s}}} \right){{\nu }_{0}}$
${{f}_{2}}=\left( \dfrac{v}{v+{{v}_{s}}} \right){{\nu }_{0}}$

Complete answer:

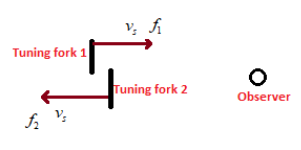
We are given two identical tuning forks each with frequency,
${{\nu }_{0}}=1400Hz$
There is a stationary observer and it is said that one of the tuning forks is approaching the observer and the other tuning fork is moving away from the observer.
Let ‘${{v}_{s}}$’ be the speed of the source.
Here tuning for is the source and it said that both the forks have equal speed and this speed is much less than the speed of sound.
Let ‘${{f}_{1}}$’ be the frequency of the sound heard by the observer from the tuning fork 1 and ‘${{f}_{2}}$’ be the frequency of sound heard by the observer from tuning fork 2.
We know that beat per second is expressed as
$\left| {{f}_{1}}-{{f}_{2}} \right|$
Now let us solve for ‘${{f}_{1}}$’ and ‘${{f}_{2}}$’.
We have frequency of tuning fork 1 heard by the observer,
${{f}_{1}}=\left( \dfrac{v}{v-{{v}_{s}}} \right){{\nu }_{0}}$, were ‘$v$’ is velocity of sound, ‘${{v}_{s}}$’ is velocity of source and ‘${{\nu }_{0}}$’ is frequency of the source.
Frequency of tuning fork 2 heard by the observer,
${{f}_{2}}=\left( \dfrac{v}{v-\left( -{{v}_{s}} \right)} \right){{\nu }_{0}}$
Here velocity of the source is negative because it is receding from the observer.
Therefore,
${{f}_{2}}=\left( \dfrac{v}{v+{{v}_{s}}} \right){{\nu }_{0}}$
Now,
$\begin{align}
  & \left| {{f}_{1}}-{{f}_{2}} \right|=\left( \dfrac{v}{v-{{v}_{s}}} \right){{\nu }_{0}}-\left( \dfrac{v}{v+{{v}_{s}}} \right){{\nu }_{0}} \\
 & \left| {{f}_{1}}-{{f}_{2}} \right|={{\nu }_{0}}v\left( \dfrac{1}{v-{{v}_{s}}}-\dfrac{1}{v-{{v}_{s}}} \right) \\
\end{align}$
In the question it is said that the observer hears 2 beats per second, i.e.
$\left| {{f}_{1}}-{{f}_{2}} \right|=2$
Therefore,
${{\nu }_{0}}v\left( \dfrac{1}{v-{{v}_{s}}}-\dfrac{1}{v-{{v}_{s}}} \right)=2$
$\begin{align}
  & {{\nu }_{0}}v\left( \dfrac{v+{{v}_{s}}-v+{{v}_{s}}}{{{v}^{2}}+{{v}_{s}}^{2}} \right)=2 \\
 & {{\nu }_{0}}v\left( \dfrac{2{{v}_{s}}}{{{v}^{2}}+{{v}_{s}}^{2}} \right)=2 \\
 & \dfrac{{{\nu }_{0}}v\times {{v}_{s}}}{{{v}^{2}}+{{v}_{s}}^{2}}=1 \\
\end{align}$
We are given that speed of source is less than speed of sound.
Therefore ${{v}_{s}}^{2}$ will be much less than that, hence we can neglect this term.
Thus,
$\dfrac{{{\nu }_{0}}v\times {{v}_{s}}}{{{v}^{2}}}=1$
Therefore we get speed of source,
$\begin{align}
  & {{v}_{s}}=\dfrac{v}{{{\nu }_{0}}} \\
 & {{v}_{s}}=\dfrac{350}{1400}=\dfrac{1}{4}m/s \\
\end{align}$
Therefore the speed of each tuning fork is $\dfrac{1}{4}m/s$.

Hence the correct answer is option D.

Note:
Beats occur when two waves of same frequencies overlap each other and form a new wave.
Beats per seconds is the difference of frequencies of the waves that are overlapping.
While calculating beats always remember to take the absolute value of difference in frequencies.