Question

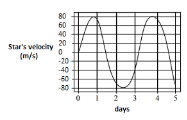
A star of mass $M$ (equal to the solar mass) with a planet (much smaller than the star) revolves around the star in a circular orbit. The velocity of the star with respect to the center of mass of the star-planet is shown below:

The radius of the planet’s orbit is closest to $\left( 1A.U.=\text{ Earth-Sun distance} \right)$

$\text{A}\text{. }0.004A.U.$
$\text{B}\text{. }0.008A.U.$
$\text{C}\text{. }0.04A.U.$
$\text{D}\text{. }0.12A.U.$

Answer 1

Hint: We will find the radius of the planet by using the equation of time period of planetary motion. We can find the formula for the time period of revolution by balancing the gravitational and centrifugal force on the planet.
Formula used:

${{T}^{2}}=\dfrac{4{{\pi }^{2}}}{GM}{{a}^{3}}$

Complete step by step answer:
All the planets in our solar system orbit around the Sun. Planets that orbit around other stars are called Exoplanets. Exoplanets are the planets beyond our own solar system.
Imagine a planet of mass$m$revolving around a star of mass$M$. Distance between their centers is$R$.

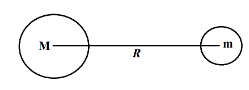
Finding the time period of revolution of a planet,
${{F}_{G}}=\dfrac{GMm}{{{R}^{2}}}$

Where,

$F$is the gravitational force between star and planet
$G$is the gravitational constant
$M$is the mass of star
$m$is the mass of planet
$R$is the distance between centers of star and planet
Now, centrifugal force experienced by the planet,

${{F}_{C}}=\dfrac{m{{v}^{2}}}{R}$

For planet to revolve with a constant speed in a circular orbit,

${{F}_{G}}={{F}_{C}}$
$\begin{align}
  & \dfrac{GMm}{{{R}^{2}}}=\dfrac{m{{v}^{2}}}{R} \\
 & {{v}^{2}}=\dfrac{GM}{R} \\
\end{align}$

Now, time period of revolution$T=\dfrac{2\pi R}{v}$

$\begin{align}
  & {{T}^{2}}=\dfrac{4{{\pi }^{2}}{{R}^{2}}}{{{v}^{2}}} \\
 & {{T}^{2}}=\dfrac{4{{\pi }^{2}}{{R}^{2}}}{\dfrac{GM}{R}} \\
 & {{T}^{2}}=\dfrac{4{{\pi }^{2}}{{R}^{3}}}{GM} \\
\end{align}$

We are given that a star of mass $M$with a planet revolves around the star in a circular orbit. We have to find the radius of orbit of the planet.
Time period of revolution of planet around the star is given by,

$\begin{align}
  & {{T}^{2}}=\dfrac{4{{\pi }^{2}}}{GM}{{a}^{3}} \\
 & \dfrac{4{{\pi }^{2}}}{GM}=1 \\
\end{align}$

$\begin{align}
  & T=\text{in year} \\
 & a\text{ = radius in }A.U. \\
\end{align}$

Therefore, \[T=3\text{ days = }\dfrac{3}{365}\text{year}\]
$a={{\left( \dfrac{3}{365} \right)}^{\dfrac{2}{3}}}$
$a=0.04A.U$
Hence, the correct option is C.

Note:
In this question, it was given that the radius of orbit of the planet is circular; therefore, we balanced the gravitational force with the centripetal force. In cases where orbit of revolution is elliptical, we cannot apply the same formula since the speed of the planet will not be constant in that case.