Question

A standing man observes rain falling with the velocity of 20m/s at an angle of 30\[{}^\circ \]with the vertical.
a. Find the velocity with which the man should move so that rain appears to fall vertically to him.
b. Now if he further increases his speed, rain again appears to fall at 30\[{}^\circ \] with the vertical. Find his new velocity.

Answer 1

Hint: This is a problem of resolution of vectors where we have to use trigonometric functions to resolve a given vector. Also, we have to find the resultant vector so we add given vectors since they are perpendicular to each other.

Complete step by step answer:
Initially, the man was at rest and after some time it had to move for him to see rain falling vertically. Let him start moving towards the left.

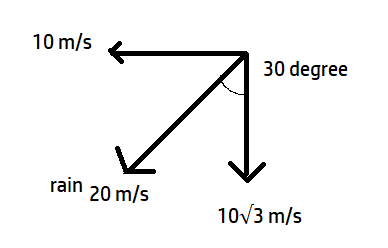
\[{{v}_{m}}=-v\overset{\scriptscriptstyle\frown}{i}\]
Resolving the rain vector,
The velocity of rain w.r.t to man, \[={{v}_{rm}}=\overrightarrow{{{v}_{r}}}-\overrightarrow{{{v}_{m}}}\]
\[={{v}_{rm}}=\overrightarrow{{{v}_{r}}}-\overrightarrow{{{v}_{m}}}\]
=\[(-10\overset{\scriptscriptstyle\frown}{i}-10\sqrt{3}\overset{\scriptscriptstyle\frown}{j})-(-{{v}_{i}})\]
\[{{v}_{rm}}=-(10-v)\overset{\scriptscriptstyle\frown}{i}-10\sqrt{3}\overset{\scriptscriptstyle\frown}{j}\]
For vertical fall, the horizontal component must be zero.
−(10−v) =0
v=10 m/s
So, the velocity with which the man should move so that rain appears to fall vertically to him is 10m/s
Now for part (B)
\[{{v}_{r}}=(-10\overset{\scriptscriptstyle\frown}{i}-10\sqrt{3}\overset{\scriptscriptstyle\frown}{j})\] m/s
Let the velocity of man in this case\[\overrightarrow{{{v}_{m}}}=-\overrightarrow{{{v}_{{}}}}\overset{\scriptscriptstyle\frown}{i}\]
The velocity of rain with respect to man
\[\overrightarrow{{{v}_{rm}}}=\overrightarrow{{{v}_{r}}}-\overrightarrow{{{v}_{m}}}\]
\[\overrightarrow{{{v}_{rm}}}=\overrightarrow{{{v}_{r}}}-\overrightarrow{{{v}_{m}}}=(-10\overset{\scriptscriptstyle\frown}{i}-10\sqrt{3}\overset{\scriptscriptstyle\frown}{j})-(-v\overset{\scriptscriptstyle\frown}{i})\]m/s
\[=(-10-v)\overset{\scriptscriptstyle\frown}{i}-10\sqrt{3}\overset{\scriptscriptstyle\frown}{j}\]
Angle with the vertical = \[30{}^\circ \]
\[\begin{align}
  & \tan 30{}^\circ =\dfrac{10-{{v}_{x}}}{-10\sqrt{3}} \\
 & {{v}_{x}}=20m/s \\
\end{align}\]
Now if he further increases his speed, rain again appears to fall at 30\[{}^\circ \]with the vertical. His new velocity is 20m/s

Note:
Special care should be taken while resolving the vectors and the sign of directions are to be included respectively as positive or negative. While taking trigonometric ratios see for angle and how it is made whether with horizontal or vertical.