Question

A square whose diagonal is 10 cm long has an area equal to
(a) 28 ${cm}^2$
(b) 34 ${cm}^2$
(c) 50 ${cm}^2$
(d) None of these

Answer 1

Hint: In this question, first let us draw the diagram with the given conditions. Then from the value of the diagonal of the square, we can get the value of the side. Now, substitute the side in the area formula to get the result.

Complete step-by-step solution -
Now, given in the question the diagonal of the square is 10 cm.

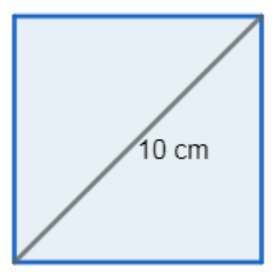
SQUARE: A rectangle is a square in which all four sides are equal. Hence, the diagonals are equal and they bisect at right angles.
Diagonal of a square is given by the formula
\[\sqrt{2}a\]
Area of a square is given by the formula
\[{{a}^{2}}\]
Let us assume the side of the square as a
Now, on comparing the given value of diagonal with the formula we get,
\[\Rightarrow \sqrt{2}a=10\]
Let us now divide with the square root of 2 on both the sides
\[\therefore a=\dfrac{10}{\sqrt{2}}\]
Now, let us find the area of the square with the above obtained side
Let us assume the area of the square as A
\[\Rightarrow A={{a}^{2}}\]
Now, on substituting the value of the side in the above formula we get,
\[\Rightarrow A={{\left( \dfrac{10}{\sqrt{2}} \right)}^{2}}\]
Now, on squaring the respective terms we get,
\[\Rightarrow A=\dfrac{100}{2}\]
Now, on further simplification we get,
\[\therefore A=50c{{m}^{2}}\]
Hence, the correct option is (c).

Note: Instead of finding the value of the side to find the area we can also get the area directly from the relation between the diagonal and area. Both methods give the same result. It is important to note that the given value in the question is diagonal not side because substituting the value of diagonal in the area formula instead of side changes the result.