Question

A square of side lies above the x-axis and has one vertex at the origin. The side passing through the origin makes an angle $\alpha \left( 0 < a < \dfrac{\pi }{4} \right)$ with the positive direction of x-axis. The equation of its diagonal not passing through the origin is

Answer 1

Hint: From the question given that we have to find the equation of the diagonal not passing through the origin of a square whose side is a and lies above the x-axis and has one vertex at the origin. To find the equation of the diagonal to find its one of the points and the slope of that diagonal. From those we will get the equation.

Complete step-by-step solution:

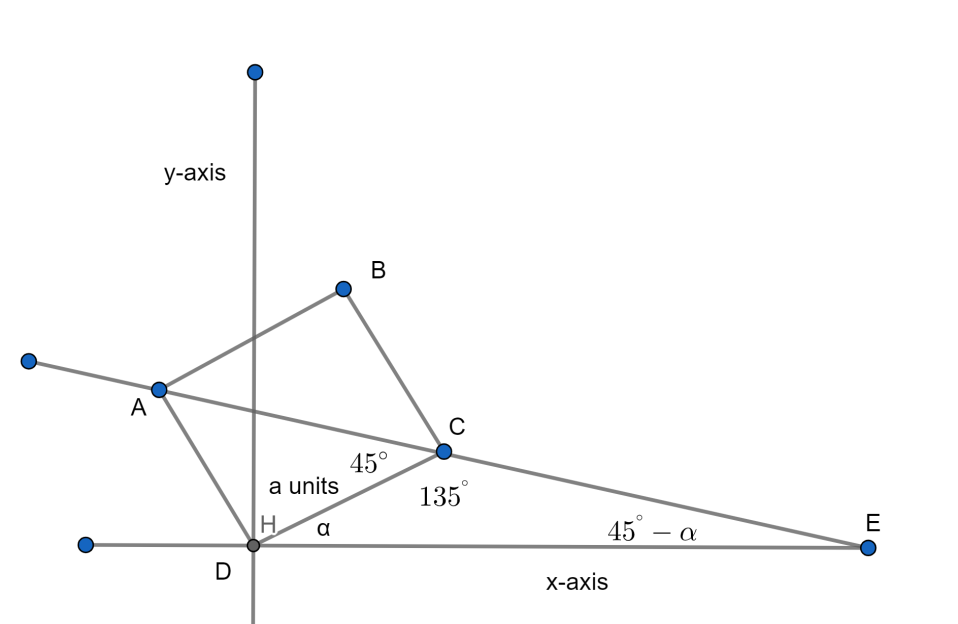
As we know that the diagonal of a square makes an angle of ${{45}^{\circ }}$ with its sides, hence
$\Rightarrow \angle DCA={{45}^{\circ }}$
Therefore, by linear pair we will get the,
$\Rightarrow \angle DCE={{135}^{\circ }}$
From the question given that the side of the square is “a”
Thus, from the co-ordinate geometry the coordinates of the vertex C will be
$\Rightarrow \left( a\cos \alpha ,a\sin \alpha \right)$
Applying sum property in the triangle DCE that is sum of all the angles in the triangle is equal to ${{180}^{\circ }}$
From this the $\angle CED$ will be,
$\Rightarrow \angle CED+\alpha +{{135}^{\circ }}={{180}^{\circ }}$
By further simplification we will get,
$\Rightarrow \angle CED={{45}^{\circ }}-\alpha $
Now the slope of the diagonal is
$\Rightarrow m=-\tan \left( \angle CED \right)$
$\Rightarrow m=-\tan \left( {{45}^{\circ }}-\alpha \right)$
As we know that
$\Rightarrow \tan \left( A-B \right)=\dfrac{\tan A-\tan B}{1+\tan A\times \tan B}$
From this the slope of the diagonal can be written as
$\Rightarrow -\tan \left( {{45}^{\circ }}-\alpha \right)=-\dfrac{1-\tan \alpha }{1+\tan \alpha }$
This can be written in terms of sin and cos we will get,
$\Rightarrow -\tan \left( {{45}^{\circ }}-\alpha \right)=-\dfrac{1-\tan \alpha }{1+\tan \alpha }=-\left( \dfrac{\cos \alpha -\sin \alpha }{\cos \alpha +\sin \alpha } \right)$
Since the diagonal passes through the vertex C, we have one point and the slope of the line the line equation will be
$\Rightarrow \dfrac{y-{{y}_{1}}}{x-{{x}_{1}}}=m$
Now substituting the values in their respective positions, we will get,
$\Rightarrow \dfrac{y-a\sin \alpha }{x-a\cos \alpha }=-\left( \dfrac{\cos \alpha -\sin \alpha }{\cos \alpha +\sin \alpha } \right)$
Now by further simplification we will get,
$\Rightarrow y\left( \cos \alpha +\sin \alpha \right)-a\sin \alpha \left( \cos \alpha +\sin \alpha \right)=-x\left( \cos \alpha -\sin \alpha \right)+a\cos \alpha \left( \cos \alpha -\sin \alpha \right)$
$\Rightarrow y\left( \cos \alpha +\sin \alpha \right)-a{{\sin }^{2}}\alpha -a\sin \alpha \cos \alpha =-x\left( \cos \alpha -\sin \alpha \right)+a{{\cos }^{2}}\alpha -a\cos \alpha \sin \alpha $
Now by further simplification we will get
$\Rightarrow y\left( \cos \alpha +\sin \alpha \right)+x\left( \cos \alpha -\sin \alpha \right)=a\left( {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha \right)$
As we know that the value of
$\Rightarrow {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1$
Therefore, from this we will get,
$\Rightarrow y\left( \cos \alpha +\sin \alpha \right)+x\left( \cos \alpha -\sin \alpha \right)=a$
Therefore, the required diagonal equation is $\Rightarrow y\left( \cos \alpha +\sin \alpha \right)+x\left( \cos \alpha -\sin \alpha \right)=a$

Note: Students any time solving like this problem first they have to convert the given question into a diagram then they can solve it easily. Students should recall all the formulas of trigonometry and coordinate geometry; this problem is a multi-conceptual. Students should be careful while doing the calculation.