Question

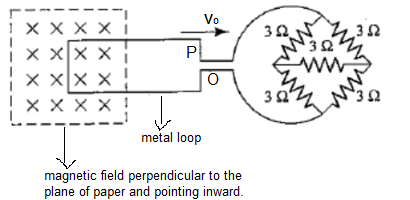
A square metal wire loop of side 10cm and resistances 1Ω is moved with a constant velocity ‘v’ in a uniform magnetic field of induction${\text{B = 2Wb}}{{\text{m}}^{ - 2}}$, as shown in the figure. The magnetic field lines are perpendicular to the plane of loop and directed into the paper. The loop is connected to the network of resistances, each of value 3Ω. The resistance of the lead wires is negligible. The speed of the loop so as to have a steady current of 1mA in the loop is?

$
  {\text{A}}{\text{. 2 m}}{{\text{s}}^{ - 1}} \\
  {\text{B}}{\text{. 2 cm}}{{\text{s}}^{ - 1}} \\
  {\text{C}}{\text{. 10 m}}{{\text{s}}^{ - 1}} \\
  {\text{D}}{\text{. 20 m}}{{\text{s}}^{ - 1}} \\
$

Answer 1

Hint: In order to find the speed of loop, we first calculate the effective resistance of the network of resistances. Using the concept of Wheatstone bridge. Then we apply the formulae of induced emf and Ohm’s law using the given data and the calculated resistance to find the answer.

Complete step-by-step solution -

Given Data,
Length of metal wire loop = 10cm = 0.1m
Current flowing in the loop i = 1 mA = 0.001 A
Magnetic field ${\text{B = 2Wb}}{{\text{m}}^{ - 2}}$
Let the speed of the loop be ‘v’.

Formula Used:
Induced emf ε = Bvl, where B is the magnetic induction, v is the speed of loop and l is the length.
Ohm’s law ε = iR, where i is the current and R is the resistance of the circuit.
First we start off by calculating the resistance of the loop –
Let’s take a look at the network of resistances given in the figure:
This looks like the figure of a Wheatstone bridge. It is an electrical circuit which is used to measure the unknown resistance of any one resistor. The voltage across both the individual series connections is equal. If we closely look at the figure we observe it looks like there are two legs which individually have two resistors connected in series, and are connected parallel to each other.
In a Wheatstone bridge we ignore the internal wire of resistance.
So here the internal wire of resistance 3Ω is removed, so the network it looks like

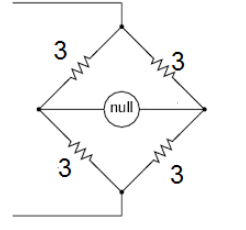
So the effective resistance of each individual half of the network is 3 + 3 = 6Ω. (as they are connected in series).
So these both effective resistances of 6Ω are connected in parallel to each other, i.e.
The effective resistance of the network becomes $\dfrac{1}{{R'}}$= $\dfrac{1}{{6}} $+ $\dfrac{1}{{6}}$⟹R’ = 3Ω.

And the metal wire has a resistance of 1Ω and it connected in series with the network of resistances. So the entire resistance of the loop becomes
R = 1 + 3 = 4Ω -- (1)

If magnetic flux in a coil is changed for whatever cause, a voltage is formed across the coil, this is also called as induced emf.
Induced emf is given by the formula ε = Bvl.
We know ohm’s law of a circuit of voltage V with a resistance R and current flowing i is given by V = iR.
Voltage can also be written as induced emf, equation both formula we get –
Given,${\text{B = 2Wb}}{{\text{m}}^{ - 2}}$, l = 0.1m and i = 0.001 A
Effective resistance of the loop = 4Ω
$
   \Rightarrow {\text{Bvl = iR}} \\
   \Rightarrow {\text{v = }}\dfrac{{{\text{iR}}}}{{{\text{Bl}}}} \\
   \Rightarrow {\text{v = }}\dfrac{{0.001 \times 4}}{{2 \times 0.1}} \\
   \Rightarrow {\text{v = 0}}{\text{.02 m}}{{\text{s}}^{ - 1}} \\
$
Hence the speed of the loop to have a steady current of 1mA is $2 \times {10^{ - 2}}{\text{m}}{{\text{s}}^{ - 1}}{\text{ or 2 cm}}{{\text{s}}^{ - 1}}$(∵1m = 100cm). Option B is the correct answer.

Note – In order to answer this type of question the key is to know the concepts of solving effective resistance using a Wheatstone bridge. The effective resistance of two resistances connected in series is given by${\text{R = }}{{\text{R}}_1}{\text{ + }}{{\text{R}}_2}$and parallel is given by$\dfrac{1}{{\text{R}}} = \dfrac{1}{{{{\text{R}}_1}}} + \dfrac{1}{{{{\text{R}}_2}}}$.
Equating voltage from ohm’s law to the induced emf is a vital step in solving this problem. Due to moving the loop with a speed in this case an emf is formed which is nothing but the voltage that causes current flowing in the loop.