Question

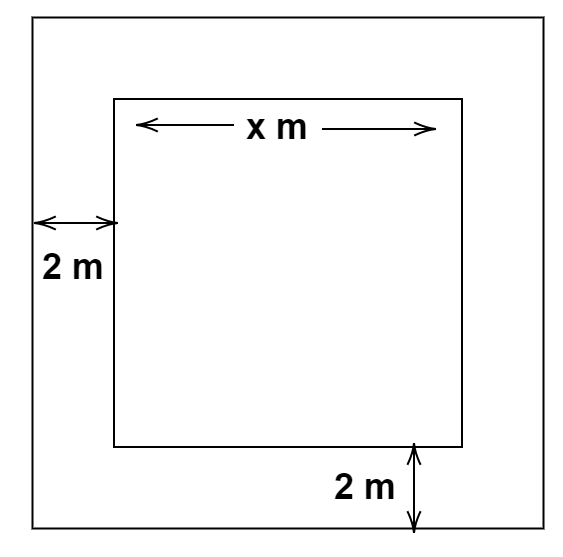
A square lawn is surrounded by a path $2m$ wide. If the area of the path is $240{m^2}$, find the area of the lawn?

Answer 1

Hint: Area of square is calculated by squaring the length of one of its sides. Area of a rectangle is calculated by multiplying its length and breadth. If we consider the above question, we have to consider two different shapes and their areas. Let us consider the length of one side of the squares as x. Then the side of the lawn including the path is $x + 2 \times 2$.
Area of lawn including the path $ = {\left( {Side} \right)^2} = {\left( {x + 4} \right)^2}$

Complete answer:
To find: ${x^2}$ (area of the lawn)
Total area that is the area of the lawn including the path is given by addition of the area of the lawn and area of the path. This can be expressed in the equation as,
Area of lawn including the path= area of the lawn + area of the path
We take the unknown value on one side and rest on another. Here the area of the lawn is unknown.
Therefore, area of the lawn= Area of lawn including the path- area of the path
Area of the lawn= area of the square $ = {x^2}$

\[{x^2} = {(x + 4)^2} - 240\]
Opening the whole square using the algebraic identity ${\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}$, we get,
 \[{x^2} = {x^2} + 8x + 16 - 240\]
Shifting the terms in the equation using method of transposition, we get,
\[{x^2} - {x^2} = 8x - 224\]
\[8x = 224\]
Dividing both sides by 8, we get,
\[x = 28\]
Therefore, the side length of the lawn is 28 meter.
So, the area of the lawn, \[{x^2} = {28^2} = 784m{}^2\]

Note:
Few things should be kept in mind when we come across such questions. Areas of square and rectangle must be known, also areas are different for square and rectangle. Also, when equal widths are added from all the sides to a square, it remains a square and the area of the new figure is the same as the area of square, i.e. square of length of one side.