Question

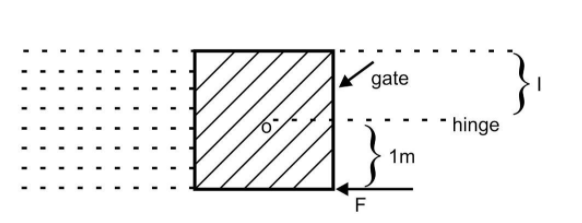
A square gate of size $2\;{\text{m}} \times 2\;{\text{m}}$ is hinged at its midpoint 0 as shown in figure. The fluid of density $\sigma $ is present to the left of the square. It is held in position by an unknown force F (Given that $\sigma $ is the density of fluid)

A) The torque exerted by the fluid in the upper half of the gate is \[\dfrac{{\sigma g}}{3}\;{\text{Nm}}\].
B) The torque exerted by the fluid in the upper half of the gate is $\dfrac{{4\sigma g}}{3}\;{\text{N}}$
C) The total force exerted by the fluid on the gate is $\dfrac{{5\sigma g}}{3}\;{\text{N}}$
D) The moment of unknown force is $\dfrac{{4\sigma g}}{3}\;{\text{Nm}}$.

Answer 1

Hint: In this question, first calculate the moment force exerted by the upper half of the gate then obtain the expression for the moment force exerted by the lower part of the gate. Now, from the moment of the upper and lower part of the gate, obtain the moment exerted by the unknown force.

Complete step by step answer:
In this question, the size of the square gate is $2\;{\text{m}} \times 2\;{\text{m}}$ hinged at O and the density of the fluid is $\sigma $.
We know that the moment of force exerted by the upper half of the gate is given by
${\tau _1} = \int\limits_0^1 {\sigma gy\left( {2dy} \right)} \left( {1 - y} \right)$
Where $\sigma gy$ is the pressure of the fluid of depth$y$, $2dy$ is the area of a layer of thickness $dy$ at $y$ and $\left( {1 - y} \right)$ is the moment arm about point $O$.
The density of the fluid and the acceleration due to gravity are constants so, the above expression can be written as,
${\tau _1} = 2\sigma g\int\limits_0^1 {\left[ {ydy - {y^2}dy} \right]} $
Now, integrate the above equation as,
${\tau _1} = 2\sigma g\left[ {\dfrac{{{y^2}}}{2} - \dfrac{{{y^3}}}{3}} \right]_0^1$
After integration apply the limits which are from $0$ to $1$ and simplify the equation as,
$\Rightarrow {\tau _1} = 2\sigma g\left( {\dfrac{1}{2} - \dfrac{1}{3}} \right) $
$\Rightarrow {\tau _1} = \dfrac{{2\sigma g}}{6} $
$\Rightarrow {\tau _1} = \dfrac{{\sigma g}}{3} $
The direction of the moment ${\tau _1}$ is clockwise.
Similarly, obtain the moment force exerted by the lower half part of the gate as,
$\Rightarrow {\tau _2} = \int\limits_0^1 {\sigma g\left( {y + 1} \right)} \left( {2dy} \right)\left( y \right)$
$ = 2\sigma g\left[ {\dfrac{1}{3} + \dfrac{1}{2}} \right] $
$ = \dfrac{{5\sigma g}}{3} $
Here, the direction of the moment is anticlockwise.
The moment exerted by the unknown force is calculated as,
$\Rightarrow \tau + {\tau _1} = {\tau _2} $
$\Rightarrow \tau = {\tau _2} - {\tau _1} $
Substitute the value of ${\tau _2}$ and ${\tau _1}$ in the above equation as,
$\tau = {\tau _2} - {\tau _1}$
$\Rightarrow \tau = \dfrac{{5\sigma g}}{3} - \dfrac{{\sigma g}}{3} $
$\Rightarrow \tau = \dfrac{{4\sigma g}}{3}\;{\text{Nm}} $

The moment of unknown force is $\dfrac{{4\sigma g}}{3}\;{\text{Nm}}$. And the torque exerted by the fluid in the upper half of the gate is \[\dfrac{{\sigma g}}{3}\;{\text{Nm}}\]. Therefore,option (A) and option (D) are correct.

Note:
In this problem, be careful about the direction of the moment. That is the direction of the moment due to the upper part of the gate is clockwise and the moment due to the lower part of the gate is an anti-clockwise direction.