Question

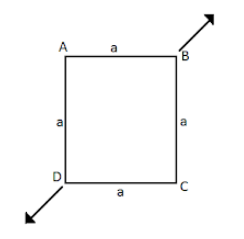
A square frame of ABCD consisting of five steel bars of cross section area $ 400m{m^2} $ and joined by pivot is subjected to action of two forces $ P = 40kN $ in the direction of the diagonal as shown. Find change in angle at $ A $ if Young’s modulus $ Y = 2 \times {10^5}N/\min $ .

 $ \left( A \right)\dfrac{1}{{2000}}rad \\
  \left( B \right)\dfrac{1}{{1000}}rad \\
  \left( C \right)\dfrac{{\sqrt 2 }}{{1000}}rad \\
  \left( D \right)\dfrac{{\sqrt 3 }}{{1000}}rad \\ $

Answer 1

Hint :In order to solve this question, we are going to construct a triangle with the help of the diagonal along which the force has been applied. After that , the angles along A in the triangle so formed are found and then they are added in order to give the total angle and then the change in angle at A.

Complete Step By Step Answer:
Let us start solving this question by first of all constructing a triangle using the diagonal line along which the force is applied as shown in this figure,

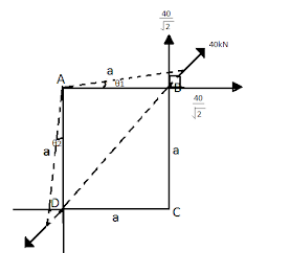
In this figure, we can see that the angle that the force vector forms with the horizontal and vertical axes is $ {45^ \circ } $ , thus, giving the horizontal and vertical components as $ \dfrac{{40}}{{\sqrt 2 }}kN $ each.
Now, the length $ x $ can be calculated as
 $ x = \dfrac{{FL}}{{AY}} $
Now, putting the values of the terms in the above formula
 $ x = \dfrac{{40 \times {{10}^3} \times 20}}{{\sqrt 2 \times 400 \times 2 \times {{10}^5}}} \\
  x = \dfrac{{{{10}^{ - 2}}}}{{\sqrt 2 }} \\ $
Now, as the angle is small, this implies,
 $ \tan \theta = \theta $
Now,
 $ \theta $ can be calculated as
 $ \theta = \dfrac{{{{10}^{ - 2}} \times \sqrt 2 }}{{20}} $
Now, the angle
 $ {\theta _1} = \theta = \dfrac{{{{10}^{ - 3}} \times \sqrt 2 }}{2} $
As we can see in the figure that,
 $ {\theta _1} = {\theta _2} $
Thus, the total angle so formed is
 $ \theta = {\theta _1} + {\theta _2} $
Putting the values in this, we get
 $ \theta = \dfrac{{{{10}^{ - 3}} \times \sqrt 2 }}{1} = \dfrac{{\sqrt 2 }}{{1000}} $
Thus, the change in angle at A is equal to $ \dfrac{{\sqrt 2 }}{{1000}} $ .

Note :
The Young modulus or the modulus of elasticity in tension, is a mechanical property that measures the tensile stiffness of a solid material. It quantifies the relationship between the force per unit area and axial strain in the linear elastic region of a material. Young's moduli are typically so large that they are expressed not in Pascals but in Gigapascals.