Question

A square current carrying loop is suspended in a uniform magnetic field acting in the plane of the loop. If the force on one arm of the loop is$\overrightarrow{F}$, the net force on the remaining three arms of the loop is
A. $3\overrightarrow{F}$
B. $-\overrightarrow{F}$
C. $-3\overrightarrow{F}$
D. $\overrightarrow{F}$

Answer 1

Hint: You could make a rough sketch of the given situation so as to have better clarity. Then, you could use the formula as per requirement. You may recall that the force for a closed loop will be zero. We are given force on one of the four arms. We could easily find the net force due to the other three arms.
Formula used:
Magnetic force,
$\overrightarrow{F}=i\left( \oint{\overrightarrow{dl}\times \overrightarrow{B}} \right)$

Complete answer:
In the question, we are given a square current carrying loop that is suspended in a uniform magnetic field that is acting in the plane of the loop. The following figure will give you a clear picture of the situation.

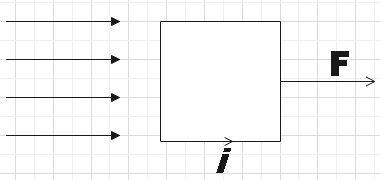
Let us recall that magnetic force could be given by,
$\overrightarrow{dF}=i\left( \overrightarrow{dl}\times \overrightarrow{B} \right)$
This expression is for a small element. Now for the whole loop it would be given by,
$\overrightarrow{F}=i\left( \oint{\overrightarrow{dl}\times \overrightarrow{B}} \right)$
We also know that, for a closed loop,
$\oint{\overrightarrow{dl}}=0$
Therefore, we could conclude that the net magnetic force would be zero for the given closed loop. We are told that the magnetic force on one of the arms is $\overrightarrow{F}$ and the net force due to the other three arms should be $-\overrightarrow{F}$ for the net force due to the loop to be zero.

Hence, option B is the correct answer.

Note:
We could define magnetic force as the attraction or repulsion that is caused by flow of current or the electrically charged particles. So, basically magnetic force is indeed a consequence of electromagnetic force. Another way to find this magnetic force is by using the magnetic Lorentz force.
$\overrightarrow{F}=q\overrightarrow{v}\times \overrightarrow{B}$