Question

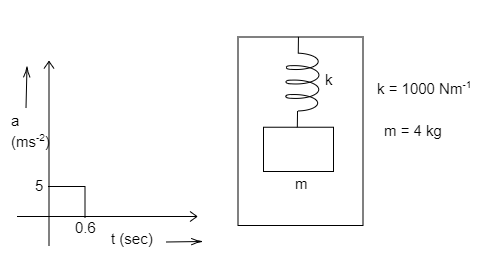
A spring block (force constant $k = 1000\,N{m^{ - 1}}$ and mass $m = 4\,kg$) system is suspended from the ceiling of an elevator such that the block is initially at rest. The elevator begins to move upwards at $t = 0$. Acceleration time graph of the elevator is shown in the figure. Draw the displacement $x$ (from its initial position taking upwards as positive) vs time graph of the block with respect to the elevator starting from $t = 0\,s$ to $t = 1\,s$. Take ${\pi ^2} = 10$

Answer 1

Hint: The displacement of the spring can be determined by using Hooke’s law. And then by using the angular frequency of the Simple harmonic motion equation, the angular frequency can be determined. Then by using the angular frequency value in simple harmonic motion formula, the graph is drawn.

Formula used:
Hooke’s law,
$F = kx$ or $ma = kx$
Where, $m$ is the mass of the block, $a$ is the acceleration, $k$ is the force constant and $x$ is the displacement of the spring.
Angular frequency of simple harmonic motion,
$\omega = \sqrt {\dfrac{k}{m}} $
Where, $\omega $ is the angular frequency, $k$ is the force constant and $m$ is the mass.
Simple harmonic motion,
$y = x\sin \left( {\omega t + \phi } \right)$
Where, $\omega $ is the angular frequency and $\phi $ is the phase angle.

Complete step by step answer:
By Hooke’s law, the stiffness is,
$F = kx$ (or) $ma = kx\,................\left( 1 \right)$
Substituting the mass, acceleration and force constant value in the above equation (1), then
$\Rightarrow 4 \times 5 = 1000 \times x$
On multiplying the above equation, then
$\Rightarrow 20 = 1000 \times x$
By keeping the term $x$ in one side and the other terms in other side, then
$\Rightarrow x = \dfrac{{20}}{{1000}}$
On dividing, then above equation is written as,
$\Rightarrow x = 0.02\,m$ or $x = 2\,cm$
Now,
Angular frequency of simple harmonic motion,
$\omega = \sqrt {\dfrac{k}{m}} \,................\left( 2 \right)$
By substituting the values of force constant and the mass in the above equation, then
$\Rightarrow \omega = \sqrt {\dfrac{{1000}}{4}} $
On dividing, then the above equation is written as,
$\Rightarrow \omega = \sqrt {250} $
The phase of the motion will lag through ${90^ \circ }$ because the motion has started $2\, cm$ below its mean position.
By the simple harmonic motion,
$y = x\sin \left( {\omega t + \phi } \right)$
Substituting the known values in the above equation, then,
$\Rightarrow y = 2\sin \left( {\sqrt {250} t + \left( { - {{90}^ \circ }} \right)} \right)$
According to trigonometry, $\sin \left( {\theta - {{90}^ \circ }} \right) = \cos \theta $, using this formula in the above equation, then,
$\Rightarrow y = 2\cos \sqrt {250} t$
By this, equation the graph will be,

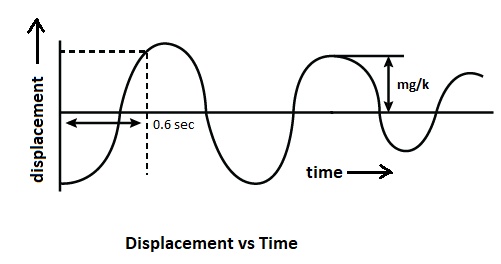
Thus, the above graph shows the displacement with respect to time.

Note:
In Hooke’s law, the force is equal to the product of force constant and displacement of the spring. But here, the force is written as the product of mass and acceleration of the object. Then, the displacement of the spring is determined.