Question

A spherical glass vessel has a cylindrical neck $8cm$ long, $2cm$ in diameter. The diameter of the spherical part is $8.5cm$. By measuring the amount of water it holds, a child finds its volume to be $345c{m^3}$. Check whether she is correct, taking the above as the inside measurement and $\pi = 3.14$.

Answer 1

Hint: In this question, you are given the measurements of a vessel which is spherical and has a cylindrical neck. We are also given the volume as measured by a student. We have to check whether the volume is correct or not. First, find the volume of the spherical part and then, find the volume of the cylindrical part. Then, add the two volumes and check if it matches the volume given in the question. If it does, the student was correct and if it does not, the student was wrong.

Complete step-by-step answer:
We are given the measurements of a spherical vessel with a cylindrical neck. We are also given the volume of the vessel as measured by a girl. We have to check whether the volume found by the girl is correct or not.
Let us assume the radius of the cylindrical neck be $r$, height be $h$, and that of the spherical vessel be $R$.

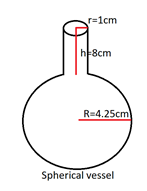
We are given that $r = 1cm$, $h = 8cm$ and $R = 4.25cm$. Using these specifications, let us find the volume of the vessel. The volume of the vessel will be found in two parts: firstly, volume of spherical part will be found and then, volume of cylindrical neck will be found.
Let us start with finding the volume of the spherical part.
Volume = $\dfrac{4}{3}\pi {r^3}$
Putting $R = 4.25cm$ and$\pi = 3.14$.
$ \Rightarrow $ Volume = $\dfrac{4}{3} \times 3.14 \times {\left( {4.25} \right)^3}$
$ \Rightarrow $ Volume = $321.4c{m^3}$
Now, we will find the volume of the second part – the cylindrical neck.
Volume = $\pi {r^2}h$
Putting $r = 1cm,h = 8cm$ and $\pi = 3.14$.
$ \Rightarrow $ Volume = $3.14 \times {1^2} \times 8$
$ \Rightarrow $ Volume = $25.12c{m^3}$
Hence, the volume of vessel = volume of spherical part + volume of cylindrical part
$ \Rightarrow $ Volume = $321.4 + 25.12 = 346.52c{m^3}$

$\therefore $ The child was incorrect.

Note: While outside mathematics the terms “sphere” and “ball” are sometimes used interchangeably, in mathematics the above distinction is made between a sphere, which is a two-dimensional closed surface embedded in a three-dimensional Euclidean space, and a ball, which is a three-dimensional shape that includes the sphere and everything inside the sphere (a closed ball) or more often, just the points inside, but not on the sphere (an open ball). The distinction between the ball and the sphere is solid. This is analogous to the situation in the plane, where the terms “circle” and “disk” can also be confused.