Question

A spherical balloon of radius r subtends an angle $\alpha $ at the eye of an observer, while the angle of elevation of its centre is $\beta $. What is the height of the centre of the balloon (neglecting the height of the observer)?
$
  {\text{A}}{\text{. }}\dfrac{{r\sin \beta }}{{\sin \left( {\dfrac{\alpha }{2}} \right)}} \\
  {\text{B}}{\text{. }}\dfrac{{r\sin \beta }}{{\sin \left( {\dfrac{\alpha }{4}} \right)}} \\
  {\text{C}}{\text{. }}\dfrac{{r\sin \left( {\dfrac{\beta }{2}} \right)}}{{\sin \alpha }} \\
  {\text{AD}}{\text{. }}\dfrac{{r\sin \alpha }}{{\sin \left( {\dfrac{\beta }{2}} \right)}} \\
 $

Answer 1

Hint- Here, we will proceed by proving that the triangles OAP and OBP are congruent to each other and this is done by using the concept that the length of the tangents drawn from any external point will always be equal.

Complete step-by-step answer:

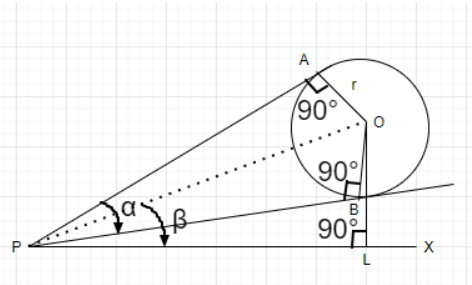
 Let O be the centre of a spherical balloon having radius r as shown in the figure.
Let point P represents the eye of an observer. In the figure shown, line PL represents the ground. Here, the height of the observer is neglected that’s why point P (eye of the observer lies at the ground). Let A and B are the point of contact between the tangents AP and BP and the spherical balloon respectively. Here, line OL is a perpendicular drawn from the centre of the spherical balloon to the ground.
Here, Radius of the spherical balloon = OA = OB = r
Given, angle subtended by the eye of an observer on the spherical balloon $\angle $APB = $\alpha $
$ \Rightarrow \angle {\text{APO}} + \angle {\text{BPO}} = \alpha {\text{ }} \to {\text{(1)}}$
Also given that, angle of elevation of the centre of the spherical balloon from the eye of the observer $\angle $OPL = $\beta $
As we know that the length of the tangents drawn from an external point will always be equal.
Since, tangents AP and BP are drawn from an external point P and hence they will be equal in length.
So, AP = BP
Also we know that the angle made between the tangent and the corresponding radius line will always be equal to ${90^0}$
For tangent AP and corresponding radius line OA, the made between these two lines must be equal to ${90^0}$ i.e., $\angle $OAP = ${90^0}$
For tangent BP and corresponding radius line OB, the made between these two lines must be equal to ${90^0}$ i.e., $\angle $OBP = ${90^0}$
In $\vartriangle $OAP and $\vartriangle $OBP, we have
OP = OP [side common to both the triangles]
$\angle $OAP = $\angle $OBP [each ${90^0}$]
OA = OB [both represents radius lines so each have value equal to r]
By SAS (Side-Angle-Side) congruence rule, these two triangles are congruent to each other
i.e., $\vartriangle $OAP$ \cong $$\vartriangle $OBP
Since, we know that in two congruent triangles any two corresponding angles will always be equal in measure.
So, $\angle $APO = $\angle $BPO
Substituting $\angle $APO = $\angle $BPO in equation (1), we get
$
   \Rightarrow \angle {\text{APO}} + \angle {\text{APO}} = \angle {\text{BPO}} + \angle {\text{BPO}} = \alpha \\
   \Rightarrow 2\angle {\text{APO}} = 2\angle {\text{BPO}} = \alpha \\
   \Rightarrow \angle {\text{APO}} = \angle {\text{BPO}} = \dfrac{\alpha }{2} \\
 $
In the right angled triangle OAP,
$
  \sin \left( {\angle {\text{APO}}} \right) = \dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}} \\
   \Rightarrow \sin \left( {\dfrac{\alpha }{2}} \right) = \dfrac{{{\text{OA}}}}{{{\text{OP}}}} \\
   \Rightarrow \sin \left( {\dfrac{\alpha }{2}} \right) = \dfrac{r}{{{\text{OP}}}} \\
   \Rightarrow {\text{OP}} = \dfrac{r}{{\sin \left( {\dfrac{\alpha }{2}} \right)}}{\text{ }} \to {\text{(2)}} \\
 $
In the right angled triangle OPL,
$
  \sin \left( {\angle {\text{OPL}}} \right) = \dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}} \\
   \Rightarrow \sin \beta = \dfrac{{{\text{OL}}}}{{{\text{OP}}}} \\
   \Rightarrow {\text{OL}} = {\text{OP}}\left( {\sin \beta } \right) \\
 $
By substituting the value of OP from equation (2) in the above equation, we get
$
   \Rightarrow {\text{OL}} = \left[ {\dfrac{r}{{\sin \left( {\dfrac{\alpha }{2}} \right)}}} \right]\left( {\sin \beta } \right) \\
   \Rightarrow {\text{OL}} = \dfrac{{r\sin \beta }}{{\sin \left( {\dfrac{\alpha }{2}} \right)}} \\
 $
Therefore, the height of the centre of the balloon from the ground is $\dfrac{{r\sin \beta }}{{\sin \left( {\dfrac{\alpha }{2}} \right)}}$
Hence, option A is correct.

Note- In any right angled triangle, the side opposite to the right angle is hypotenuse, the side opposite to the considered angle is perpendicular and the remaining side is base. Here, in the right angled triangle OAP, OP is hypotenuse, OA is perpendicular and AP is the base whereas in the right angled triangle OPL, OP is hypotenuse, OL is perpendicular and PL is base.