Question

A spherical ball of mass $m$and radius $r$rolls without slipping on a rough concave surface of large radius $R$. It makes small oscillations about the lowest point. Find the time period.

Answer 1

Hint: We know that when a spherical ball of mass $m$and radius $r$rolls without slipping on a rough concave surface of large radius $R$, it executes simple harmonic motion. In simple harmonic motion, total energy remains constant. Therefore we will use this concept to solve this problem.

Formula used:
$v = r\omega $, where $v$ is the linear velocity, $r$is the radius of circular motion and $\omega $is the angular velocity
$\alpha = \theta {\omega ^2}$, where $\alpha $is the angular acceleration, $\theta $is the angular displacement and $\omega $is the angular velocity
$I = \dfrac{2}{5}m{r^2}$ , where $I$is the moment of inertia of spherical body, $m$is the mass of spherical body and $r$is the radius of the spherical body
$T = \dfrac{{2\pi }}{\omega }$, where $T$ is the time period and $\omega $is the angular velocity

Complete step by step answer:
It is given that a spherical ball of mass $m$and radius $r$rolls without slipping on a rough concave surface of large radius $R$ as shown in figure.

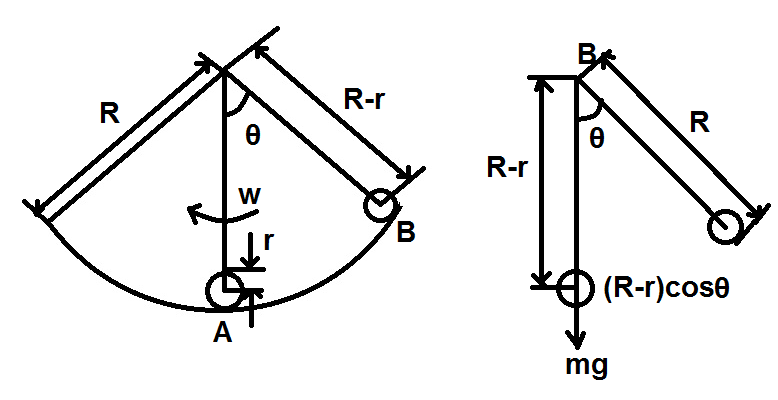
Now, Let us take $\omega $ as the angular velocity of the system about the point of suspension at any time. Therefore, by using the formula $v = r\omega $ , the velocity of the ball rolling on a rough concave surface is given as
${v_c} = \left( {R - r} \right)\omega $
If we take as $\omega '$ the rotational velocity of sphere, then
$
  {v_c} = r\omega ' \\
   \Rightarrow \omega ' = \dfrac{{{v_c}}}{r} = \dfrac{{\left( {R - r} \right)\omega }}{r} \\
 $
Now, we know that total energy o the particle executing simple harmonic motion remains constant.
\[ \Rightarrow mg\left( {R - r} \right)\left( {1 - \cos \theta } \right) + \dfrac{1}{2}m{v_c}^2 + \dfrac{1}{2}I\omega {'^2} = C\]
Where, C is constant
Now we will put the values of \[{v_c}\], $\omega '$and $I$in this equation
\[
   \Rightarrow mg\left( {R - r} \right)\left( {1 - \cos \theta } \right) + \dfrac{1}{2}m{\left( {R - r} \right)^2}{\omega ^2} + \dfrac{1}{2}\left( {\dfrac{2}{5}m{r^2}} \right){\left( {\dfrac{{R - r}}{r}} \right)^2}{\omega ^2} = C \\
   \Rightarrow mg\left( {R - r} \right)\left( {1 - \cos \theta } \right) + \dfrac{1}{2}m{\left( {R - r} \right)^2}{\omega ^2} + \dfrac{1}{5}m{r^2}{\left( {\dfrac{{R - r}}{r}} \right)^2}{\omega ^2} = C \\
   \Rightarrow g\left( {R - r} \right)\left( {1 - \cos \theta } \right) + {\left( {R - r} \right)^2}{\omega ^2}\left( {\dfrac{1}{2} + \dfrac{1}{5}} \right) = C \\
   \Rightarrow g\left( {R - r} \right)\left( {1 - \cos \theta } \right) + \dfrac{7}{{10}}{\left( {R - r} \right)^2}{\omega ^2} = C \\
 \]
Taking derivative with respect to time both the sides,
$ \Rightarrow g\left( {R - r} \right)\left( { - \sin \theta } \right)\dfrac{{d\theta }}{{dt}} + \dfrac{7}{{10}}{\left( {R - r} \right)^2}2\omega \dfrac{{d\omega }}{{dt}} = 0$
We know that $\dfrac{{d\theta }}{{dt}}$=$\omega $ and $\dfrac{{d\omega }}{{dt}} = \alpha $
$ \Rightarrow g\sin \theta = \dfrac{7}{5}\left( {R - r} \right)2\alpha $
As the value of $\theta $is very small, we can take $\sin \theta = \theta $
\[
   \Rightarrow g\theta = \dfrac{7}{5}\left( {R - r} \right)2\alpha \\
   \Rightarrow \alpha = \dfrac{{5g\theta }}{{7\left( {R - r} \right)}} \\
 \]
We know that
$\alpha = \theta {\omega ^2}$
\[
   \Rightarrow {\omega ^2} = \dfrac{{5g}}{{7\left( {R - r} \right)}} \\
   \Rightarrow \omega = \sqrt {\dfrac{{5g}}{{7\left( {R - r} \right)}}} \\
 \]
The time period is given by
$T = \dfrac{{2\pi }}{\omega }$
$ \Rightarrow T = 2\pi \sqrt {\dfrac{{7(R - r)}}{{5g}}} $

Note:
Here, we have determined the time period in the case of spherical ball rolling without slipping on a concave surface. This time period is dependent on radii of ball as well as the concave surface and the gravitational acceleration. We know that the frequency is the inverse of the time period. Therefore frequency in this case is given by $f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{5g}}{{7(R - r)}}} $ .