Question

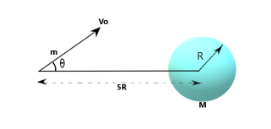
A spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the center of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. The angle $\theta $ for which the package just grazes the surface of the planet is

A.)${\sin ^{ - 1}}\left( {\dfrac{1}{2}\sqrt {1 + \dfrac{{2GM}}{{5v_0^2R}}} } \right)$
B.)${\sin ^{ - 1}}\left( {\dfrac{1}{5}\sqrt {1 + \dfrac{{8GM}}{{5v_0^2R}}} } \right)$
C.)${\sin ^{ - 1}}\left( {\dfrac{1}{8}\sqrt {1 + \dfrac{{3GM}}{{5v_0^2R}}} } \right)$
D.)${\sin ^{ - 1}}\left( {\dfrac{1}{3}\sqrt {1 + \dfrac{{6GM}}{{5v_0^2R}}} } \right)$

Answer 1

Hint: In this question we first apply the conservation of angular momentum at the center of the planet because there is no external unbalancing torque present that is $m{v_o}5R\sin \theta = mvR$ from here we get the relation between $v$ and ${v_o}$ as $5{v_o}\sin \theta = v$ . Now we apply the conservation of energy as $\dfrac{1}{2}mv_o^2 - \dfrac{{GMm}}{{5R}} = \dfrac{1}{2}m{v^2} - \dfrac{{GMm}}{R}$ to get the answer.


Complete answer:
First we need to draw the trajectory of the package that is shown in figure 1 with the red line.

Now we can see that there is no external unbalancing torque present in the system of planet and package. Therefore we can apply the conservation of momentum at the center of the planet that is

$m{v_o}5R\sin \theta = mvR$
Here $v$ is the velocity when the package grazes the surface

         ${v_o}$ is the velocity at which the package is fired
         $m$ is mass of the package
         $\theta $ the angle with the perpendicular at which the package is fired
        $R$ is radius of the planet

Now by canceling the m and R on both side we get the relation between $v$ and ${v_o}$ that is

$ \Rightarrow m{v_o}5R\sin \theta = mvR$
$ \Rightarrow 5{v_o}\sin \theta = v$------------------------------------ (1)

Now using the conservation of energy that is the sum of initial potential and kinetic energy is equal to the sum of final potential and kinetic energy of a system. This is because energy can neither be created nor be destroyed.

${\left( {PE + KE} \right)_{initial}} = {\left( {PE + KE} \right)_{final}}$

$\dfrac{1}{2}mv_o^2 - \dfrac{{GMm}}{{5R}} = \dfrac{1}{2}m{v^2} - \dfrac{{GMm}}{R}$------------------------- (2)

Substituting equation number (1) in equation (2) we will get

$ \Rightarrow \dfrac{1}{2}mv_o^2 - \dfrac{{GMm}}{{5R}} = \dfrac{1}{2}m{\left( {5{v_o}\sin \theta } \right)^2} - \dfrac{{GMm}}{R}$”

Canceling $m$ on both side we will get

$ \Rightarrow \dfrac{1}{2}mv_o^2 - \dfrac{{GMm}}{{5R}} = \dfrac{1}{2}m{\left( {5{v_o}\sin \theta } \right)^2} - \dfrac{{GMm}}{R}$

$ \Rightarrow \dfrac{1}{2}v_o^2 - \dfrac{{GM}}{{5R}} = \dfrac{{25}}{2}v_o^2{\sin ^2}\theta - \dfrac{{GM}}{R}$

Taking ${v_o}$ in one side and G terms on other side we get

$ \Rightarrow \dfrac{{GM}}{R} - \dfrac{{GM}}{{5R}} = \dfrac{{25}}{2}v_o^2{\sin ^2}\theta - \dfrac{1}{2}v_o^2$
$ \Rightarrow \left( {\dfrac{{25}}{2}{{\sin }^2}\theta - \dfrac{1}{2}} \right)v_o^2 = \dfrac{{4GM}}{{5R}}$

$ \Rightarrow \left( {\dfrac{{25{{\sin }^2}\theta - 1}}{2}} \right)v_o^2 = \dfrac{{4GM}}{{5R}}$
$ \Rightarrow \left( {\dfrac{{25{{\sin }^2}\theta - 1}}{2}} \right) = \dfrac{{4GM}}{{5v_o^2R}}$
$ \Rightarrow 25{\sin ^2}\theta - 1 = \dfrac{{8GM}}{{5v_o^2R}}$
$ \Rightarrow 25{\sin ^2}\theta = 1 + \dfrac{{8GM}}{{5v_o^2R}}$

Taking square root on both side we get

$ \Rightarrow 5\sin \theta = \sqrt {1 + \dfrac{{8GM}}{{5v_o^2R}}} $
$ \Rightarrow \sin \theta = \dfrac{1}{5}\sqrt {1 + \dfrac{{8GM}}{{5v_o^2R}}} $
$ \Rightarrow \theta = {\sin ^{ - 1}}\left( {\dfrac{1}{5}\sqrt {1 + \dfrac{{8GM}}{{5v_o^2R}}} } \right)$

Therefore we get the angle for which the package grazes the planet’s surface as $\theta = {\sin ^{ - 1}}\left( {\dfrac{1}{5}\sqrt {1 + \dfrac{{8GM}}{{5v_o^2R}}} } \right)$ . So option B is correct.

Note: For these types of question we need to have a clear understanding of different laws like conservation of mass, conservation of angular momentum, conservation of energy. We need to know how and when to apply these concepts. We also need to know Newton's laws of motion. In these types of questions, always take care of the sign convention.