Question

A space is filled up with volume charge density $\rho = {\rho _0}{e^{ - \alpha {r^3}}}$ where ${\rho _0}$ and $\alpha $ are positive constants, r is the distance from the centre of the system. The magnitude of electric field strength as a function of r is given as $\dfrac{{{\rho _0}}}{{x{\varepsilon _0}\alpha {r^2}}}\left( {1 - {e^{ - \alpha {r^3}}}} \right)$ . Find x.

Answer 1

Hint: We can solve this problem using gauss law. According to gauss law the flux through a closed surface is $\dfrac{1}{{{\varepsilon _0}}}$ times the charge enclosed by it. Using the gauss law equation, we can calculate the electric field. By comparing it with the equation for the electric field given in the question we can find the value of x.

Complete step by step answer:
It is given that a space is filled with volume charge density
$\rho = {\rho _0}{e^{ - \alpha {r^3}}}$
Where ${\rho _0}$ and $\alpha $ are positive constants.
 The distance from the centre of the system is given as r.
We need to calculate the magnitude of electric field strength as a function of r so that we can find the value of x.
Let us use gauss law to find the electric field.
we know that according to gauss law the flux through a closed surface will be equal to $\dfrac{1}{{{\varepsilon _0}}}$ times the total charge enclosed by the closed surface.
Here we can consider a spherical surface of radius r as the gaussian surface.
Gauss law can be written as
$\oint_S {E_n dA = \frac{1}{{\varepsilon _0 }}} Q_{inside}$ (1)
Where, E is the electric field and q is the total charge enclosed.
The volume charge density is the charge per unit volume
So, the total charge enclosed can be found by multiplying the volume charge density with volume.
$ \Rightarrow q = \int \rho dV$
Where, $\rho $ is the volume charge density and V is the volume.

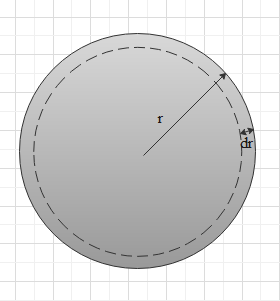
If we consider sphere with radius $r$ and thickness $dr$, then the volume can be written as
$dV = 4\pi {r^2} \times dr$
Where, $4\pi {r^2}$ is the surface area of the sphere.
So, we get,
$ \Rightarrow q = \int\limits_0^r {\rho \times 4\pi {r^2}dr} $
$ \Rightarrow q = \int\limits_0^r {{\rho _0}{e^{ - \alpha {r^3}}} \times 4\pi {r^2}dr} $
$ \Rightarrow q = \dfrac{{4\pi {\rho _0}}}{3}\int\limits_0^r {3{r^2}{e^{ - \alpha {r^3}}}dr} $
Let us find the value of the integral
$I = \int\limits_0^r {3{r^2}{e^{ - \alpha {r^3}}}dr} $
Let us put
$ - \alpha {r^3} = t$
On taking the derivative on both sides, we get
$ \Rightarrow - 3{r^2}dr = \dfrac{{ - dt}}{\alpha }$
When $r = 0$ , $t = 0$
When $r = r$ , $t = - \alpha {r^3}$
We can write the integral in terms of t as
$I = \int\limits_0^{ - \alpha {r^3}} {{e^t}\dfrac{{ - dt}}{\alpha }} $
$ \Rightarrow I = \dfrac{{ - 1}}{\alpha }\int\limits_0^{ - \alpha {r^3}} {{e^t}dt} $
$ \Rightarrow I = \dfrac{{ - 1}}{\alpha }\left[ {{e^t}} \right]_0^{ - \alpha {r^3}}$
$ \Rightarrow I = \dfrac{{ - 1}}{\alpha }\left[ {{e^{ - \alpha {r^3} - {e^0}}}} \right]$
$ \Rightarrow I = \dfrac{1}{\alpha }\left[ {1 - {e^{ - \alpha {r^3}}}} \right]$
On substituting the value of integral in equation for charge enclosed, we get
$ \Rightarrow q = \dfrac{{4\pi {\rho _0}}}{3}\dfrac{1}{\alpha }\left[ {1 - {e^{ - \alpha {r^3}}}} \right]$
Now let us substitute this value in equation 1.


$ \Rightarrow E \times 4\pi {r^2} = \dfrac{{4\pi {\rho _0}}}{{3\alpha {\varepsilon _0}}}\left[ {1 - {e^{ - \alpha {r^3}}}} \right]$
$ \Rightarrow E = \dfrac{{4\pi {\rho _0}}}{{3\alpha {\varepsilon _0} \times 4\pi {r^2}}}\left[ {1 - {e^{ - \alpha {r^3}}}} \right]$
$ \Rightarrow E = \dfrac{{{\rho _0}}}{{3{\varepsilon _0}\alpha {r^2}}}\left( {1 - {e^{ - \alpha {r^3}}}} \right)$ (2)
In the question the value of electric field is given as
$E = \dfrac{{{\rho _0}}}{{x{\varepsilon _0}\alpha {r^2}}}\left( {1 - {e^{ - \alpha {r^3}}}} \right)$ (3)
On comparing equation 3 and 2 we can see that the value of x is 3.
$\therefore x = 3$

Note: Remember that gauss is not applicable in all cases. It is applied in situations where there is some symmetry in the charge distribution. The gaussian surface that is considered should also have some symmetry like the charge distribution so the electric field is constant across the gaussian surface.