Question

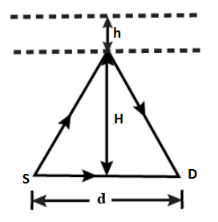
A source $ S $ and a detector $ D $ of high frequency waves are a distance $ d $ apart on the ground. The direct wave from $ S $ is found to be in phase at $ D $ with the wave from $ S $ that is reflected rays making the same angle with the reflecting layer. When the layer rises a distance $ h $ , no signal is detected at $ D $ . Neglect absorption in the atmosphere and find the relation between $ d $ , $ h $ , $ H $ and the wavelength $ \lambda $ of the waves.

Answer 1

Hint :In order to solve this question, we are going to consider the two rays that are approaching the point $ D $ first from the height $ H $ and then from the height $ \left( {H + h} \right) $ . The first one will form constructive interference and the latter will be destructive. Thus, respective path differences are subtracted.
The path difference for constructive interference is given by
 $ \Delta x = n\lambda $
The path difference for destructive interference is given by
 $ \Delta x = \left( {n + \dfrac{1}{2}} \right)\lambda $ .

Complete Step By Step Answer:
If we observe the situation as given in the question, we see that when a ray is reflected from a height $ H $ , and the other one comes to $ D $ in a direct way, then, the interference that occurs is a constructive one.
We know that the path difference for constructive interference is given by
 $ \Delta x = n\lambda $
Where,
 $ n = 0,1,2,3,.... $
Let us consider a point P at the height $ H $
Thus, $ SD = d $
 $ SP = \sqrt {{H^2} + {{\left( {\dfrac{d}{2}} \right)}^2}} $
And, $ PD = \sqrt {{H^2} + {{\left( {\dfrac{d}{2}} \right)}^2}} $
Hence, $ SP + PD = 2\sqrt {{H^2} + {{\left( {\dfrac{d}{2}} \right)}^2}} = \sqrt {4{H^2} + {d^2}} $
Hence, the path difference is given by
 $ \Delta x = SP - SD = \sqrt {4{H^2} + {d^2}} - d \\
   \Rightarrow n\lambda = \sqrt {4{H^2} + {d^2}} - d - - - - \left( 1 \right) \\ $
When ray comes from height $ H + h $ , there is no direct ray coming to $ D $ , then the destructive interference occurs at $ D $
Now, path difference for destructive interference is given by
 $ \Delta x = \left( {n + \dfrac{1}{2}} \right)\lambda $
Where, $ n = 0,1,2,3,.... $
Let us consider a point Q at the height $ H + h $
 $ SD = d $
And
  $ SQ = \sqrt {{{\left( {H + h} \right)}^2} + {{\left( {\dfrac{d}{2}} \right)}^2}} \\
  QD = \sqrt {{{\left( {H + h} \right)}^2} + {{\left( {\dfrac{d}{2}} \right)}^2}} \\ $
Thus, $ SQ + QD = 2\sqrt {{{\left( {H + h} \right)}^2} + {{\left( {\dfrac{d}{2}} \right)}^2}} = \sqrt {4{{\left( {H + h} \right)}^2} + {d^2}} $
Hence, the path difference is given by
 $ SQ - SD = \sqrt {4{{\left( {H + h} \right)}^2} + {d^2}} - d \\
   \Rightarrow \left( {n + \dfrac{1}{2}} \right)\lambda = \sqrt {4{{\left( {H + h} \right)}^2} + {d^2}} - d - - - - \left( 2 \right) \\ $
Subtracting equation $ \left( 1 \right) $ from equation $ \left( 2 \right) $
 $ \lambda = 2\sqrt {4{{\left( {H + h} \right)}^2} + {d^2}} - 2\sqrt {4{H^2} + {d^2}} $

Note :
For both the constructive and the destructive interference, two factors that remain common are the variable $ n $ and the wavelength, the respective relations for both the types are different which gives two different equations and thus, helps to solve for the value of the wavelength.