Question

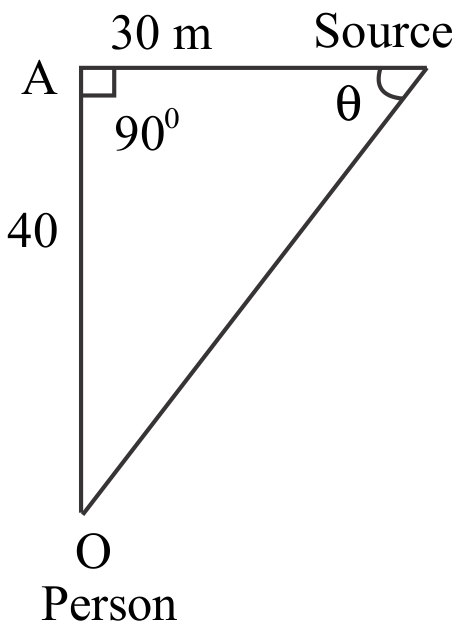
A source of the sound of frequency 640 Hz is moving at a velocity of $\dfrac{{100}}{3}$m/s along a road, and is at an instant \[30m\] away from a point A on the road (as shown in the figure). A person standing at O, 40m away from the road hears the sound of apparent frequency v’. the value of v’ is:
(velocity of sound =\[340{\text{ }}m/s\]).

A) 620 Hz
B) 680 Hz
C) 720 Hz
D) 840 Hz

Answer 1

Hint: Doppler effect can be considered as a property of sound wave. It is a change in sound wave frequency caused by the relative movement of either source, Listener, or both. Use the equation of the doppler effect to find the respective frequencies heard by the listener when the source of the sound of frequency 640Hz is moving at a velocity of $\dfrac{{100}}{3}$m/s.

Complete step by step solution:
When a source of sound approaches us the pitch becomes higher and as it moves away from the listener, the pitch gets lower. It is due to the change in the number of waves passing through per unit area per unit time,i.e due to the frequency. As someone approaches a stationary listener the sound waves compress which increases the frequency resulting in the higher pitch. Similarly, as the source moves away, the number of waves decreases as it spreads apart therefore frequency will decrease giving a lower pitch. Similarly, when the source and listener approach each other the frequency increases and they move apart the frequency decreases.
Considering the influencing factors such as the speed of listener or source, either it is approaching or going further away the equation of doppler effect can be written as
V’=$\dfrac{{\mathop v\nolimits_a }}{{\mathop v\nolimits_a - \mathop v\nolimits_s }}$v
This is the case of doppler effect with source approaching the observer. The velocity of approach of source towards observer is = $v\cos \theta = \dfrac{{100}}{3}\cos \theta = \dfrac{{100}}{3} \times \dfrac{3}{5} = 20$m/s
hence
v’=$\dfrac{{\mathop v\nolimits_a }}{{\mathop v\nolimits_a - \mathop v\nolimits_s }}v$
v=640m/s
$\mathop v\nolimits_a = 340$m/s , $\mathop v\nolimits_s = 20$m/s
=$640\left( {\dfrac{{340}}{{340 - 20}}} \right) = 680$Hz

The value of v’ is 680 Hz. So, the correct answer is option (B).

Note:
Similarly, the doppler effect is also seen in light as well. Due to that any light moving towards the observer will be shifted to lower wavelengths. This is called a blue shift. Similarly, light sources moving far away from the observer will shift to longer wavelengths. This is called a red shift. Since the speed of all the EMW is relatively very large as compared to the speed of source or listener in our day to day life, the apparent change in frequency is not easily noticed. The apparent frequency is almost equal to its original frequency.