Question

A solid sphere of radius R rolls without slipping on the floor with linear momentum p. Its angular momentum with respect to a point on the floor is
A. $2pR/5$
 B. $pR/5$
C. $pR/7$
D. $7pR/5$

Answer 1

Hint: This question is based on the rotational motion. The easiest way to solve this kind of question is to compare with linear motion. The formulas which we apply for the linear motion can be applied here just by interchanging the terms. Linear acceleration can be interchanged with angular acceleration and linear velocity with angular velocity and linear displacement with angular displacement. We use a parallel axis theorem to solve this.
Formula used:
$I = {I_C} + m{r^2}$
$v = R\omega $
$L = I\omega $
$p = mv$

Complete answer:
Solid sphere is performing the pure rolling motion without slipping on the floor. We are asked to find out the angular momentum with respect to the point on the ground.
We have the formula for the angular momentum $(L)$ as $L = I\omega $
Where $I$ is the moment of inertia of the point about which we need angular momentum and $\omega $ is the angular velocity of the body which will be constant for every point of the rolling body.

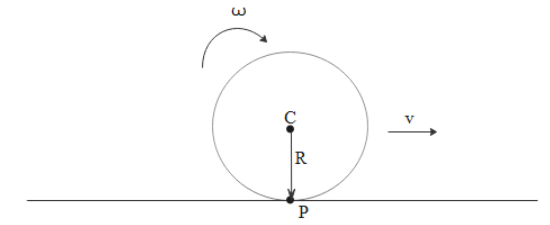
Since we need angular momentum about point P we should find out the moment of inertia about point P first by using parallel axes theorem. Which is
$I = {I_C} + m{r^2}$
Where
${I_C}$ is the moment of inertia about an axis passing through center of the sphere
$I$ is the moment of inertia about the point we need, here it is P
$m$ is the mass of the sphere
$r$ is the distance between the axis passing through center and the axis passing through point P
We know for a solid sphere ${I_C} = \dfrac{2}{5}m{R^2}$ where R is the radius of the sphere
$I = {I_C} + m{r^2}$ we have $r = R$
$\eqalign{
  & \Rightarrow I = \dfrac{2}{5}m{R^2} + m{R^2} \cr
  & \Rightarrow I = \dfrac{7}{5}m{R^2} \cr} $
Now we should find the angular velocity. For the case of pure rolling we have $v = R\omega $
Where $v$is the linear velocity and $\omega $ is the angular velocity
$v = R\omega $
$ \Rightarrow \omega = \dfrac{v}{R}$ …eq1
Linear momentum will be $p = mv$
$p = mv$
$ \Rightarrow v = \dfrac{p}{m}$
By substituting velocity value in equation 1 we get
$\omega = \dfrac{p}{{mR}}$
Angular momentum will be $L = I\omega $ and by substituting the values we get
$L = I\omega $
$\eqalign{
  & \Rightarrow L = \dfrac{7}{5}m{R^2}(\dfrac{p}{{mR}}) \cr
  & \Rightarrow L = \dfrac{{7pR}}{5} \cr} $

Hence option D will be the correct answer.

Note:
In case of pure rolling the velocity of point of contact with respect to the ground will be zero. This is the reason why we can consider the rolling motion of an object as a pure rotatory motion with respect to the point of contact and it is also called as the instantaneous center of the rotation.