Question

A solid sphere, a hollow sphere and a ring are released from top of an inclined plane (frictionless) so that they slide down the plane. Then maximum acceleration down the plane is for (no rolling):
A. Solid sphere
B. Hollow sphere
C. Ring
D. All same

Answer 1

Hint: We are given a solid sphere, a hollow sphere and a ring. It is said that all these three bodies are released from the top of an inclined plane and there is no friction on any surfaces and also that the bodies are not rolling. We know that when there is no friction the only force acting will be gravitational force. By this concept we can solve the question.

Complete step by step answer:
In the question we are given an inclined plane and it is said that a solid sphere, a hollow sphere and a ring is released from the top of the plane.
Consider the figure given below.

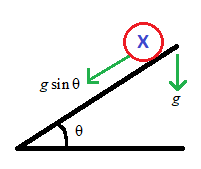
‘X’ in the figure represents the solid sphere, the hollow sphere and the ring.
In the question it is said that the surface is frictionless.
Therefore the coefficient of friction is zero, which means that the frictional force will also be zero.
Hence the only force acting on all the three bodies will be the gravitational force.
We know that gravitational force acts vertically downwards.
Therefore, from the figure we can find the component of ‘g’ in the direction of the inclined plane, which is the maximum acceleration of the three bodies.
Therefore we have maximum acceleration of all three bodies; the solid sphere, the hollow sphere and the ring
${{a}_{\max }}=g\sin \theta $, were ‘${{a}_{\max }}$’ is the maximum acceleration, ‘g’ is gravitational acceleration and ‘$\theta $’ is the angle of inclination of the plane.
From this we can understand that the maximum acceleration on this inclined plane is only dependent on the angle of inclination of the plane and the gravitational acceleration.
We know that gravitational acceleration and angle of inclination are constant.
Therefore the maximum acceleration of all the three bodies; the solid sphere, the hollow sphere and the ring are the same.
Hence the correct answer is option D.

Note:
We know that when a body falls down an inclined plane the forces acting on the body are the frictional force and the gravitational force.
We know that frictional force, $F=\mu g$.
In the given situation, it is said that all the surfaces are frictionless.
Therefore we have coefficient of friction, i.e. $\mu =0$
Therefore the frictional force,
$\begin{align}
  & F=0\times g \\
 & F=0 \\
\end{align}$
Hence the only force acting on the body will be the gravitational force.