Question

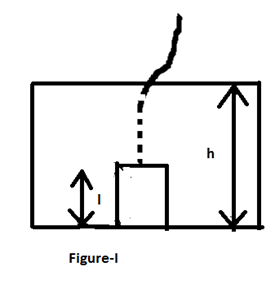
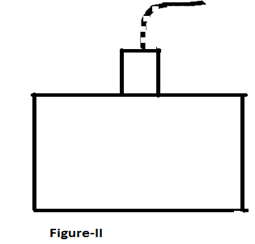
A solid right cylinder of length l stands upright on the bottom of a large tub filled with water up to height as shown in the figure –I. Density of the material of the cylinder equals that of water. Now the cylinder is pulled slowly out of the water with the help of a thin light inextensible thread as shown in figure –II. Find the work done by the tension force developed in the thread.
      

A. $mgh$
B. $mgl$
C. $0.5mgl$
D. $mg(0.5l+h)$

Answer 1

Hint: Here we have to consider the different forces acting on the cylinder, here we have two forces, one is the weight of the cylinder and other one is the upthrust applied by the liquid on the cylinder. We have to evaluate the net force acting on the body and the displacement of the body and then we can calculate the work done by the tension.

Complete answer:
As the density of the cylinder and the water is the same, no force will act on the cylinder up to the time the whole cylinder is inside the water. But when the cylinder starts to come out from the water, a net force will start to act on it. Let at any instant length x is out of the water as shown in the diagram.

 

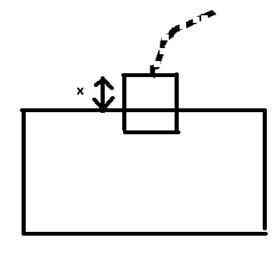
Let the cross sectional area of the cylinder be $A$ and the density is $\rho $. Now at this instant the net force required to pull the cylinder upwards is given by
Weight of the cylinder $-$ upthrust on it
$=Al\rho g-A(l-x)\rho g=Ax\rho g$.
Now the work done to lift the cylinder further by a small length $dx$ is given by
$dw=Ax\rho g\times dx$
So the total work done to lift the cylinder is given by
$w=\int\limits_{0}^{l}{Ax\rho g\times dx=A\rho g\int\limits_{0}^{l}{\left( xdx \right)}}=\dfrac{1}{2}A\rho {{l}^{2}}g$.
Now mass of the cylinder is given by
$m=Al\rho $
Now putting the value of $m$ in the equation of $w$ we get
$w=\dfrac{1}{2}mgl=0.5mgl$

Note:
Here the Archimedes’ principle is applied. It states that the apparent weight loss of a body when immersed in a liquid is equal to the weight of the liquid displaced by the body. In this problem first we need to calculate the work for very small displacement and then we will have to integrate it. Otherwise we will have the wrong answer because here the force is also changing.