Question

A solid metallic right circular cone 20cm height whose vertical angle is ${60^0}$, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum is so obtained to be drawn into a wire of diameter 1/12 cm, find the length of the wire?

Answer 1

Hint: Here we go through by first making the diagram of a right circular cone and then bisecting it at the middle of its height and by the properties of trigonometry we will find the radius of frustum of cone. And then equate the volume of frustum of cone to the volume of cylindrical wire.

Complete step-by-step answer:
Here in the question it is given that a solid metallic right circular cone 20cm height whose vertical angle is${60^0}$, is cut into two parts at the middle of its height by a plane parallel to its base.
Now we have to first draw the diagram according to the question.

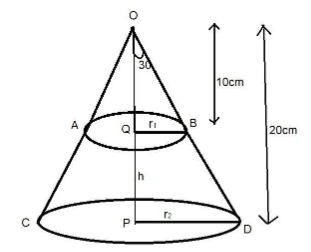
Now let, OCD be the metallic cone and ABDC be the required frustum.
In the question it is given that the height of the cone is 20cm.
And let the radius of upper circle be ${r_1}$and lower circle be ${r_2}$
Through the figure we can say that $\angle QOB = \angle POD = {30^0}$ because the perpendicular line bisect the angle of cone.
Now by applying the trigonometry properties we can write it as,
$\tan {30^0} = \dfrac{{PD}}{{OP}}$ And $\tan {30^0} = \dfrac{{QB}}{{OB}}$ as we know $\tan \theta $ is the ratio of perpendicular to base.
Now by putting the values we get,
$\tan {30^0} = \dfrac{1}{{\sqrt 3 }} = \dfrac{{{r_2}}}{{20}}$ And $\tan {30^0} = \dfrac{1}{{\sqrt 3 }} = \dfrac{{{r_1}}}{{10}}$
${r_2} = \dfrac{{20}}{{\sqrt 3 }}cm,{r_1} = \dfrac{{10}}{{\sqrt 3 }}$
Now as we know the volume of frustum of cone is $\dfrac{1}{3}\pi h({r_1}^2 + {r_2}^2 + {r_1}{r_2})$
Now by putting the values in the formula we get,
$
   = \dfrac{{\pi \times 10}}{3}\left( {{{\left( {\dfrac{{20}}{{\sqrt 3 }}} \right)}^2} + {{\left( {\dfrac{{10}}{{\sqrt 3 }}} \right)}^2} + \left( {\dfrac{{20}}{{\sqrt 3 }}} \right) \times \left( {\dfrac{{10}}{{\sqrt 3 }}} \right)} \right) \\
   = \dfrac{{10\pi }}{3}\left( {\dfrac{{900}}{3} + \dfrac{{100}}{3} + \dfrac{{200}}{3}} \right) \\
   = \dfrac{{10\pi }}{3}\left( {\dfrac{{700}}{3}} \right) = \dfrac{{7000\pi }}{3}c{m^3} \\
 $
And in the question it says that the cylindrical wire is made from the frustum of cone it means that the volume of frustum of cone is equal to the volume of cylindrical wire.
And in the question it is given that the diameter of wire is $\dfrac{1}{{12}}m$
Volume of wire = volume of frustum
$
   \Rightarrow \pi {r^2}h = \dfrac{{7000\pi }}{3} \\
   \Rightarrow h = \dfrac{{7000}}{3} \times {\left( {\dfrac{1}{{\dfrac{1}{{24}}}}} \right)^2} = 7964.4m \\
  \therefore h = 7964.4m \\
 $
Hence the required length of wire is 7964.4m

Note: Whenever we face such a type of question the key concept for solving the question is to first find out the volume of new shapes that are cut out from the old shape. By applying the properties of trigonometry relation. We will also apply here the property of a similar triangle to find out the radius of the frustum of cone. And then solve it by just comparing the volume of each figure.