Question

A solid is in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is 3.5 cm and the height of the cone is 4 cm. The solid is placed in a cylindrical vessel, full of water, in such a way that the whole solid is submerged in the water. If the radius of the cylindrical vessel is 5 cm and its height is 10.5 cm, find the volume of water left in the cylindrical vessel?

Answer 1

Hint: To solve the above question, we will first find the volume of that solid which is going to be submerged in water. For this, we will find the volume of the cone and the volume of the hemisphere. The sum of their volumes will be equal to the volume of the solid. Then we will find the volume of the water which will be equal to the volume of the cylindrical vessel. Then we will make use of the fact that when the solid is submerged in water, the volume of water left will be equal to the difference in volumes of the solid and the cylinder.

Complete step-by-step answer:
In the question, it is given that there is a solid which is made by mounting a right circular cone on a hemisphere and that this solid is placed in a cylindrical vessel full of water, in such a way that the whole solid is submerged in the water. So, the given situation can be shown as follows.

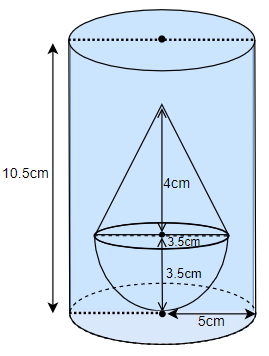
The first thing we are going to do is to calculate the volume of this solid. The volume of the solid will be equal to the sum of the volumes of the cone and the cylinder. So, we will calculate the volumes of the cone and the hemisphere individually.
The volume of the cone with a radius of base ‘r’ and height ‘h’ is given by:
\[\text{Volume }=\dfrac{1}{3}\pi {{r}^{2}}h\]
In our case, r is equal to the radius of the hemisphere, i.e. r = 3.5 cm and h = 4 cm. Thus, we will get,
\[\text{Volume of the cone }=\dfrac{1}{3}\times \pi \times {{\left( 3.5 \right)}^{2}}\times 4c{{m}^{3}}\]
\[\Rightarrow \text{Volume of the cone }=\dfrac{1}{3}\times \pi \times \left( \dfrac{7}{2}\times \dfrac{7}{2} \right)\times 4c{{m}^{3}}\]
\[\Rightarrow \text{Volume of the cone }=\dfrac{49\pi }{3}c{{m}^{3}}\]
The volume of the hemisphere with radius ‘r’ is given by the formula shown below.
\[\text{Volume }=\dfrac{2}{3}\times \pi {{r}^{3}}\]
In our case, \[r=3.5c{{m}^{3}}.\] Thus, we will get,
\[\text{Volume of the hemisphere}=\dfrac{2}{3}\times \pi \times {{\left( 3.5 \right)}^{3}}c{{m}^{3}}\]
\[\Rightarrow \text{Volume of the hemisphere}=\dfrac{2}{3}\times \pi \times \left( \dfrac{7}{2}\times \dfrac{7}{2}\times \dfrac{7}{2} \right)c{{m}^{3}}\]
\[\Rightarrow \text{Volume of the hemisphere}=\dfrac{343\pi }{12}c{{m}^{3}}\]
Now, we will calculate the volume of the solid which is equal to the sum of the volumes of the hemisphere and the cone. Thus,
\[\text{Volume of solid}=\left( \dfrac{49\pi }{3}+\dfrac{343\pi }{12} \right)c{{m}^{3}}\]
\[\Rightarrow \text{Volume of solid}=\left( \dfrac{196\pi +343\pi }{12} \right)c{{m}^{3}}\]
\[\Rightarrow \text{Volume of solid}=\dfrac{539\pi }{12}c{{m}^{3}}\]
Now, we will calculate the volume of water which is equal to the volume of the cylindrical vessel. The volume of the cylinder with radius ‘r’ and height ‘h’ is given by
\[\text{Volume }=\pi {{r}^{2}}h\]
In our case, h = 10.5 cm and r = 5 cm. Thus, we have,
\[\text{Volume of water }=\text{Volume of cylinder}=\pi \times {{\left( 5 \right)}^{2}}\times 10.5c{{m}^{3}}\]
\[\Rightarrow \text{Volume of water }=\pi \times 25\times \dfrac{21}{2}c{{m}^{3}}\]
\[\Rightarrow \text{Volume of water }=\dfrac{525\pi }{2}c{{m}^{3}}\]
Now, it is given that the solid is submerged in water. We will make use of the fact that the volume of water displaced by the solid will be equal to the volume of the solid. Thus, we can say that,
\[\text{Volume of water displaced}=\dfrac{539\pi }{12}c{{m}^{3}}\]
Now, we know that the volume of water will be the sum of the volume of water displaced and the remaining volume. Thus, we will get,
Volume of water = Volume of water displaced + Remaining water volume
\[\Rightarrow \dfrac{525\pi }{2}c{{m}^{3}}=\dfrac{539\pi }{12}c{{m}^{3}}+\text{ remaining water volume}\]
\[\Rightarrow \text{Remaining water volume}=\dfrac{525\pi }{2}c{{m}^{3}}-\dfrac{539\pi }{12}c{{m}^{3}}\]
\[\Rightarrow \text{Remaining water volume}=\dfrac{\pi }{2}\left( 525-\dfrac{539}{6} \right)c{{m}^{3}}\]
\[\Rightarrow \text{Remaining water volume}=\dfrac{\pi }{2}\left( \dfrac{3150-530}{6} \right)c{{m}^{3}}\]
\[\Rightarrow \text{Remaining water volume}=\dfrac{2611\pi }{12}c{{m}^{3}}\]
\[\Rightarrow \text{Remaining water volume}=\dfrac{2611}{12}\times \dfrac{22}{7}c{{m}^{3}}\]
\[\Rightarrow \text{Remaining water volume}=\dfrac{4103}{6}c{{m}^{3}}\]
\[\Rightarrow \text{Remaining water volume}=683.83c{{m}^{3}}\]

Note:
While solving this question, we have assumed that the cylindrical vessel is hollow and it has negligible thickness. Due to this assumption, the volume of water is equal to the volume of the cylinder. Also, we have assumed that the cone which is mounted on the hemisphere in the solid has a radius equal to the volume of the cone.