Question

A solid has a BCC. Structure. If the distance of the closest approach between the two atoms is\[\text{1}\text{.73 Angstrom}\] . The edge length of the cell is (approx.):
A) \[\text{200 pm}\]
B)$\frac{\sqrt{3}}{\sqrt{2}}\text{pm}$
C) \[\text{142}\text{.2 pm}\]
D) $\sqrt{\text{2}}\text{pm}$

Answer 1

Hint: For BCC structure the radius of the atom ‘r’ and the edge length of the cubic structure ‘a’ are related as:
$\text{r = }\frac{\sqrt{3}\text{a}}{4}$. Use this relation to obtain the answer.

Complete answer:
We are provided with the following data:
a) The Solid has a BCC structure
b) The distance between the atoms,
$\text{2r = 1}\text{.73 }\overset{\text{0}}{\mathop{\text{A}}}\,$
c) To find edge length is ‘a’
-We know that in the BCC structure the atoms are present on the corners of the cubic unit cell and one of the atoms is located at the centre of the body. They are arranged in such a way that the atoms which are on the corners and at the centre of the body are touching each other.
The body-centered cubic structure as follows:

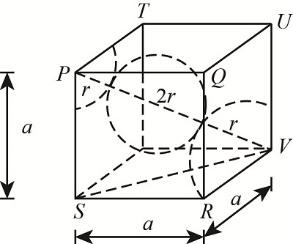
Here ‘a’ represents the length of the edge and ‘r’ is the radius of an atom
The distance between the two atoms $\text{= 2r = 1}\text{.73}\overset{\text{0}}{\mathop{\text{A}}}\,$
Therefore, $\text{= r = }\frac{\text{1}\text{.73}\overset{\text{0}}{\mathop{\text{A}}}\,}{2}=0.865\text{ }\overset{\text{0}}{\mathop{\text{A}}}\,$
For BCC structure, lets us relate the radius ‘r’ with the edge length ‘a’.
The body diagonal PV is composed of a body centered atom and the two atoms at the corners.
Thus, $\text{body diagonal (PV)= r + 2r + r = 4r}$
Let's consider a triangle $\text{ }\!\!\Delta\!\!\text{ SVR}$ ,
Apply Pythagoras theorem. We have,
${{\text{(SV)}}^{\text{2}}}\text{=(SR}{{\text{)}}^{\text{2}}}\text{+(VR}{{\text{)}}^{\text{2}}}$
Where SV is face diagonal. We know that,
$\text{SR=RV=edge length=a}$
Thus,
$\begin{align}
  & {{\text{(SV)}}^{\text{2}}}\text{=(a}{{\text{)}}^{\text{2}}}\text{+(a}{{\text{)}}^{\text{2}}} \\
 & \text{ = 2}{{\text{a}}^{2}} \\
\end{align}$
Let us apply the Pythagoras theorem in $\text{ }\!\!\Delta\!\!\text{ PSV}$
${{\text{(PV)}}^{\text{2}}}\text{=(PS}{{\text{)}}^{\text{2}}}\text{+(SV}{{\text{)}}^{\text{2}}}$
Substitute the value. We get,
$\begin{align}
  & {{\text{(PV)}}^{\text{2}}}\text{=(a}{{\text{)}}^{\text{2}}}\text{+(2a}{{\text{)}}^{\text{2}}} \\
 & \text{ = 3}{{\text{a}}^{\text{2}}} \\
\end{align}$
Substitute PV we get,
$\begin{align}
  & {{\text{(PV)}}^{\text{2}}}\text{=(a}{{\text{)}}^{\text{2}}}\text{+(2a}{{\text{)}}^{\text{2}}} \\
 & \text{ = 3}{{\text{a}}^{\text{2}}} \\
 & \text{PV=}\sqrt{\text{3}}\text{a} \\
\end{align}$
Equate the values for PV. We have,
$\text{4r = 3a}$
$\text{r = }\frac{\sqrt{3}\text{a}}{4}$ or $\frac{4}{\sqrt{3}}\text{r = a}$
On substitution values we get,
$\begin{align}
  & \text{a=}\frac{\text{4}}{\sqrt{\text{3}}}\text{ }\!\!\times\!\!\text{ (0}\text{.865 }\overset{\text{0}}{\mathop{\text{A}}}\,\text{)} \\
 & \text{a=1}\text{.99 }\overset{\text{0}}{\mathop{\text{A}}}\,\text{ }\simeq \text{ 2}\text{.0 }\overset{\text{0}}{\mathop{\text{A}}}\, \\
\end{align}$

The angstrom can be converted into the picometer.
$\text{2}\text{.0 }\overset{\text{0}}{\mathop{\text{A}}}\,=200\text{ pm}$

Hence, (A) is the correct option.

Note:
Do not get confused with the FCC and BCC solid structure. In BCC one atom is at the centre of the body and the other at the corners. However in the FCC structure each face has an atom along with the corners of the body.