Question

A solid cylinder rolls up on an inclined plane of an angle of inclination $ {30^0} $ . At the bottom of the inclined plane, the center of mass of the cylinder has a speed of $ 5m/s $ .
1. How far will the cylinder go up the plane?
2. How long will it take to return to the bottom?

Answer 1

Hint: The angle of inclination and the velocity with which the cylinder moves upward is also given. We can use the law of conservation of mechanical energy and form an equation. And from this equation, we can find the height reached by the cylinder. Once we find the height using the trigonometric formula we can find the displacement of the cylinder.

Complete answer:

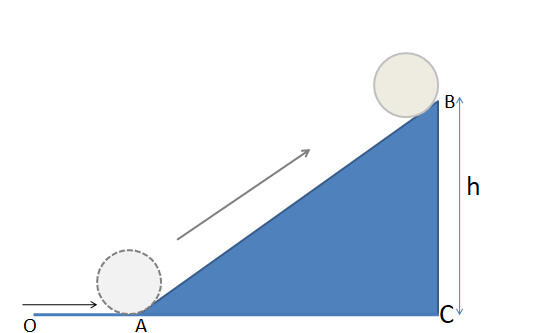
The cylinder is moving upwards. The angle of inclination $ \theta $ $ = 3{0^0} $
We know from the law of conservation of mechanical energy, the potential energy is equal to the kinetic energy.
The energy of the cylinder at the starting point is,
 $ K.{E_{rot}} + K.{E_{trans}} = 0 $
We know the formula for both the rotational and kinetic energy,
 $ \dfrac{1}{2}I{\omega ^2} + \dfrac{1}{2}m{v^2} = 0 $ ………… (1)
This equation (1) will be equal to the potential energy at the final position of the cylinder
 $ P.E = mgh $ ……… (2)
Equating equations (1) and (2)
 $ \dfrac{1}{2}I{\omega ^2} + \dfrac{1}{2}m{v^2} = mgh $ …………. (3)
The Formula for the moment of inertia of the solid cylinder is given as,
 $ I = \dfrac{1}{2}m{r^2} $ ……… (4)
Substituting equation (4) in equation (3)
 $ \dfrac{1}{2}(\dfrac{1}{2}m{r^2}){\omega ^2} + \dfrac{1}{2}m{v^2} = mgh $
Simplifying the above equation we get,
 $ \dfrac{1}{4}m{r^2}{\omega ^2} + \dfrac{1}{2}m{v^2} = mgh $
Also, we have the relation between the angular velocity and the linear velocity as
 $ v = r\omega $ ……….. (5)
Substituting (5) in the above equation we get,
 $ \dfrac{1}{4}m{v^2} + \dfrac{1}{2}m{v^2} = mgh $
Canceling the $ m $ term on both sides of the equation,
 $ \dfrac{1}{4}{v^2} + \dfrac{1}{2}{v^2} = gh $
 $ \Rightarrow \dfrac{3}{4}{v^2} = gh $
 $ \Rightarrow h = \dfrac{3}{4}\dfrac{{{v^2}}}{g} $
Substituting for $ v = 5m/s $ and $ g = 9.8 $
 $ h = \dfrac{3}{4} \times \dfrac{{5 \times 5}}{{9.8}} $
 $ \Rightarrow h = 1.91m $
From the triangle in the above diagram,
 $ \sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}} $
Here hypotenuse is the total displacement of the cylinder therefore we can say it as $ s $
Opposite is the height $ h $ , rearranging the above formula to find out $ s $
 $ s = \dfrac{h}{{\sin \theta }} $
 $ \Rightarrow s = \dfrac{{1.91m}}{{\sin {{30}^0}}} $
 $ \Rightarrow s = 3.82m $
Time taken to return to the bottom is given by,
 $ t = \dfrac{s}{v} $
 $ \Rightarrow t = \dfrac{{AB}}{{{{(\dfrac{4}{3} \times g \times AB\sin \theta )}^{1/2}}}} = {(\dfrac{{3AB}}{{4g\sin \theta }})^{1/2}} $
 $ \Rightarrow t = {(\dfrac{{11.46}}{{19.6}})^{1/2}} = 0.764s $
Therefore the time taken for the cylinder to come back to the original position is
 $ 2 \times 0.764s = 1.53s $ .

Note:
Note that the formula for the time taken from the following derivation,
For the radius of gyration K, the velocity of the cylinder at the instant when it rolls back to the bottom is given by the relation:
 $ v = {\left( {\dfrac{{2gh}}{{1 + \dfrac{{{K^2}}}{{{R^2}}}}}} \right)^{1/2}} $
 $ \Rightarrow v = {\left( {\dfrac{{2gAB\sin \theta }}{{1 + \dfrac{{{K^2}}}{{{R^2}}}}}} \right)^{1/2}} $
But we know that for a solid cylinder $ {K^2} = \dfrac{{{R^2}}}{2} $ , substituting this in the above equation we get,
 $ v = {\left( {\dfrac{{2gAB\sin \theta }}{{1 + \dfrac{1}{2}}}} \right)^{1/2}} $
 $ \Rightarrow v = {(\dfrac{4}{3}gAB\sin \theta )^{1/2}} $
This given velocity will be substituted in the time formula.