Question

A solid cylinder of mass M rolls without slipping down on an inclined plane making an angle \[\theta \] with the horizontal. The acceleration of the cylinder down the inclined plane is
A. \[\dfrac{2}{3}g\sin \theta \]
B. \[\dfrac{3}{2}g\sin \theta \]
C. \[g\sin \theta \]
D. \[g\]

Answer 1

Hint: Drawing the free body diagram of the forces acting on the body, you will get the acceleration term. Recall the formula for the torque and acceleration in rolling motion. Solving these three equations, you will get the expression for the acceleration. Using the moment of inertia of the cylinder in the acceleration term, you will get the acceleration in terms of only acceleration due to gravity and angle of inclination.

Formula used:
\[\tau = I\alpha \]
Here, \[\tau \] is the torque, I is the moment of inertia of the cylinder and \[\alpha \] is the rotational acceleration of the cylinder.

Complete step by step answer:
Let us find the acceleration of the cylinder over an inclined plane by balancing the forces acting on the ball.

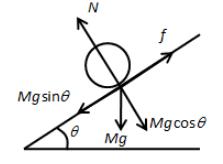
From the above free body diagram, we can write,
\[Mg\sin \theta - f = Ma\] …… (1)
Here, M is the mass of the cylinder, g is the acceleration due to gravity, f is the frictional force and a is the acceleration.
For the rotational motion of the cylinder, we can write,
\[\tau = fR = I\alpha \] …… (2)
Here, \[\tau \] is the torque, R is the radius of the cylinder, I is the moment of inertia of the cylinder and \[\alpha \] is the rotational acceleration of the cylinder.

For the rolling motion of the ball, the acceleration of the ball is,
\[a = R\alpha \] …… (3)
Substituting the value of f from equation (2) in equation (1), we get,
\[Mg\sin \theta - \dfrac{{I\alpha }}{R} = Ma\]
Substituting the value of \[\alpha \] from equation (3) in the above equation, we get,
\[Mg\sin \theta - \dfrac{{Ia}}{{{R^2}}} = Ma\]
\[ \Rightarrow Mg\sin \theta = Ma + \dfrac{{Ia}}{{{R^2}}}\]
\[ \Rightarrow g\sin \theta = a\left( {1 + \dfrac{I}{{M{R^2}}}} \right)\]
\[ \Rightarrow a = \dfrac{{g\sin \theta }}{{1 + \dfrac{I}{{M{R^2}}}}}\] …… (4)

We have the moment of inertia of the cylinder of mass M and radius R,
\[I = \dfrac{{M{R^2}}}{2}\]
Using the above equation in equation (4), we get,
\[a = \dfrac{{g\sin \theta }}{{1 + \dfrac{{M{R^2}}}{{2M{R^2}}}}}\]
\[ \Rightarrow a = \dfrac{{g\sin \theta }}{{1 + \dfrac{1}{2}}}\]
\[ \therefore a = \dfrac{2}{3}g\sin \theta \]

So, the correct answer is option A.

Note: Remember, the direction of the frictional force is always opposite to the direction of the motion. While solving these types of questions, the essential step is to draw the free body diagram and equate the forces acting on the body. Students should remember the expressions for the moment of inertia of the frequently used objects such as ring, disk, cylinder, rod, etc.