Question

A solid cylinder of mass 50kg and radius 0.5m is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other hanging freely. Tension in the string required to produce an angular acceleration of 2 $ { revolutions }/{ { s }^{ -2 } }$ is:-
A. 25 N
B. 50 N
C. 78.5 N
D. 157 N

Answer 1

Hint: Use the formula of torque in terms of tension and radius. But we know, torque is also related to angular acceleration and inertia. Now, write inertia in terms of mass and radius. Substitute the values and calculate tension in the string.

Formula used:
$ \tau \quad =\quad T\quad \times \quad r$
$ \tau \quad =\quad I\quad \times \quad \alpha$
$ I\quad =\quad \dfrac { m{ R }^{ 2 } }{ 2 }$

Complete answer:
Given: Mass of solid cylinder (m) = 50kg
Radius of cylinder (R)= 0.5m
Angular acceleration ($\alpha$)= $ 2\quad { rev }/{ { s }^{ -2 } }$ = $ 2\quad \times \quad 2\pi { { rad }/{ { s }^{ -2 } } }$

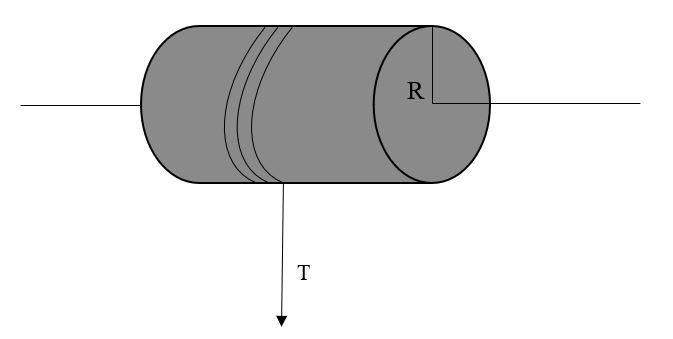
Torque is given by,
$ \tau \quad =\quad T\quad \times \quad r$ …(1)
where, $\tau$ : Torque
T : Tension in the string
R: Radius of cylinder

Rearranging equation.(1) we get,
$ T=\quad \dfrac { \tau }{ R }$ …(2)
We know, $ \tau \quad =\quad I\quad \times \quad \alpha$
Therefore, equation.(2) becomes
$ T\quad =\quad \dfrac { I\quad \times \quad \alpha }{ R }$
where, I: Rotational Inertia
But, $ I\quad =\quad \dfrac { m{ R }^{ 2 } }{ 2 }$
$ \Rightarrow T\quad =\quad \dfrac { m{ R }^{ 2 } }{ 2 } \times \quad \dfrac { \alpha }{ R }$
$ \Rightarrow T\quad =\quad \dfrac { m{ R }\alpha }{ 2 }$
$ \Rightarrow T\quad =\quad \dfrac { 50\quad \times \quad { 0.5\quad \times \quad }4\pi }{ 2 }$
$ \Rightarrow T\quad =\quad 157.08$
Therefore, tension in the string required to produce an angular acceleration of 2 revolutions $ { s }^{ -2 }$ is 157N.

So, the correct answer is “Option D”.

Note:
Make sure you convert unit of angular acceleration from $ { revolutions }/{ { s }^{ -2 } }$ to $ { { rad }/{ { s }^{ -2 } } }$. There are 2$\pi$ radians in a complete revolution. So to get total angular acceleration, multiply $ { revolutions }/{ { s }^{ -2 } }$ with $ 2\pi { { rad }/{ { s }^{ -2 } } }$.